题目内容
已知平行六面体ABCD-A′B′C′D′中，AB=4，AD=3，AA′=5，∠BAD=90°，∠BAA′=∠DAA′=60°，（1）求AC′的长；（如图所示）
（2）求
| AC/ |
| AC |
分析：（1）可得
=
+
=
+
+
，由数量积的运算可得|
|2，开方可得；（2）由（1）可知|
|，又可求|
|和
′•
，代入夹角公式可得．
| AC′ |
| AC |
| CC′ |
| AB |
| AD |
| AA′ |
| AC′ |
| AC′ |
| AC |
| AC |
| AC |
解答：解：（1）可得
=
+
=
+
+
，
故|
|2=|
+
+
|2=
2+
2+
2
+2（
•
+
•
+
•
）
=42+32+52+2（4×3×0+4×5×
+3×5×
）=85
故AC′的长等于|
|=
（2）由（1）可知
=
+
+
，|
|=
故
′•
=（
+
+
）•（
+
）
=
2+2
•
+
2+
•
+
•
=42+2×4×3×0+32+5×4×
+5×3×
=
又|
|=
=
=
=5
故
与
的夹角的余弦值=
=
=
| AC′ |
| AC |
| CC′ |
| AB |
| AD |
| AA′ |
故|
| AC′ |
| AB |
| AD |
| AA′ |
| AB |
| AD |
| AA′ |
+2（
| AB |
| AD |
| AB |
| AA′ |
| AD |
| AA′ |
=42+32+52+2（4×3×0+4×5×
| 1 |
| 2 |
| 1 |
| 2 |
故AC′的长等于|
| AC′ |
| 85 |
（2）由（1）可知
| AC′ |
| AB |
| AD |
| AA′ |
| AC′ |
| 85 |
故
| AC |
| AC |
| AB |
| AD |
| AA′ |
| AB |
| AD |
=
| AB |
| AB |
| AD |
| AD |
| AA′ |
| AB |
| AA′ |
| AD |
=42+2×4×3×0+32+5×4×
| 1 |
| 2 |
| 1 |
| 2 |
| 85 |
| 2 |
又|
| AC |
(
|
|
| 42+0+32 |
故
| AC/ |
| AC |
| ||||
|
|
| ||
|
| ||
| 10 |
点评：本题考查空间向量的模长和夹角的余弦值的运算，化向量为
，
，
是解决问题的关键，属中档题．
| AB |
| AD |
| AA′ |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
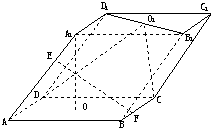如图，已知平行六面体ABC-A1B1C1的底面为正方形，O1，O分别为上、下底面中心，且A1在底面ABCD上的射影为O．
如图，已知平行六面体ABCD-A1B1C1D1．
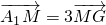，设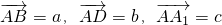
，用向量a、b、c表示向量
；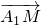