Question

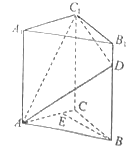
【题目】如图，直三棱柱中，，为棱上一点，，为线段上一点，.

（Ⅰ）证明：平面；

（Ⅱ）若，求四棱锥的体积.

Answer 1

【答案】（Ⅰ）详见解析（Ⅱ）

【解析】试题分析：（Ⅰ）证明线面平行，一般方法为利用线面平行判定定理，即从线线平行出发给予证明，而线线平行的寻找与论证，往往结合平几知识，如本题构造平行四边形，利用平行四边形性质得线线平行（Ⅱ）求棱锥的体积，关键是求高，而高的探求实质是利用线面垂直关系，本题可由直三棱柱得侧面与底面垂直，再根据面面垂直性质定理转化为线面垂直，即得锥的高，最后代入锥的体积公式即可.

试题解析：（Ⅰ）证明：如图，过点作交于点，连接.

由，故，得.

由，故，

又，故.

所以四边形为平行四边形，从而.

又平面，平面，

故平面.

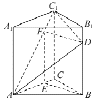
（Ⅱ）解：由已知，因为，

则中，，

中，.

由知为等腰三角形，设底边上的高为，

则，

，

所以四棱锥的体积.