题目内容
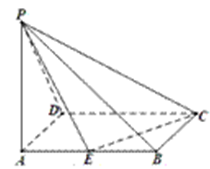
如图,在四棱锥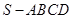 中,底面
中,底面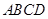 是正方形,
是正方形,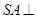 底面
底面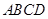 ,
,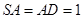 ,点
,点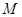 是
是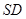 的中点,
的中点,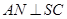 ,交
,交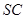 于点
于点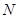 .
.
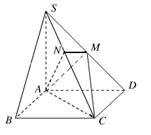
(1)求证:平面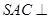 平面
平面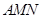 ;
;
(2)求三棱锥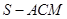 的体积.
的体积.
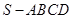 中,底面
中,底面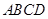 是正方形,
是正方形,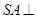 底面
底面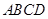 ,
,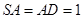 ,点
,点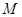 是
是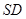 的中点,
的中点,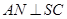 ,交
,交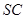 于点
于点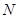 .
.
(1)求证:平面
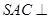 平面
平面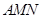 ;
;(2)求三棱锥
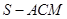 的体积.
的体积.(1)详见解析;(2)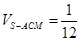 .
.
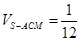 .
.试题分析:(1)求证:平面
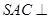 平面
平面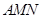 ,证明两个平面垂直,只需证明一个平面过另一个平面的垂线即可,注意到已知
,证明两个平面垂直,只需证明一个平面过另一个平面的垂线即可,注意到已知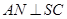 ,可想到证明
,可想到证明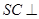 面
面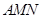 ,只需证明
,只需证明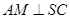 ,或
,或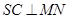 ,但
,但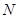 位置不确定,可考虑证
位置不确定,可考虑证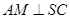 ,由已知点
,由已知点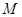 是
是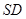 的中点,已知
的中点,已知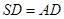 ,故
,故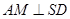 ,而四棱锥
,而四棱锥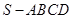 的底面
的底面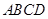 是正方形,
是正方形,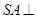 底面
底面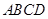 ,故
,故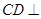 面
面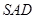 ,这样能得到
,这样能得到 面
面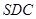 ,从而得
,从而得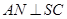 ,问题得证;(2)求三棱锥
,问题得证;(2)求三棱锥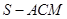 的体积,由于
的体积,由于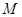 是
是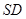 的中点,则
的中点,则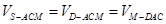 ,这样转化为求
,这样转化为求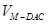 ,由图可知,
,由图可知,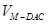 容易求出.
容易求出.试题解析:(1)∵
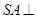 底面
底面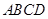 ,∴
,∴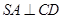
又
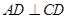 ∴
∴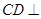 面
面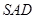
∴
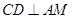 ······① 3分
······① 3分又
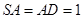 ,且
,且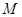 是
是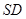 的中点,∴
的中点,∴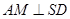 ·········②
·········②由①②得
 面
面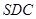 ∴
∴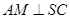
又
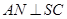 ∴
∴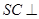 面
面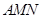
∴平面
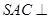 平面
平面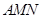 6分
6分(2)∵
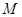 是
是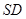 的中点,∴
的中点,∴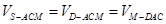 . 9分
. 9分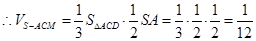 12分
12分
练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
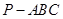 中,
中,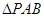 和
和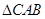 都是以
都是以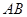 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,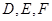 分别是
分别是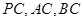 的中点.
的中点.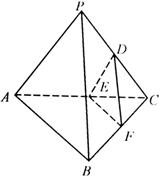
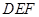 //平面
//平面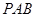 ;
;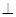
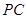 ;
;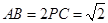 ,求三棱锥
,求三棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且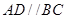 ,
, ,平面
,平面 底面
底面 为
为 的中点,
的中点, 是棱
是棱 的中点,
的中点, .
.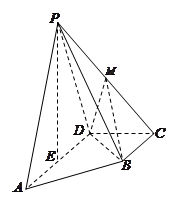

 平面
平面 ;
; 的体积.
的体积.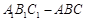 中,侧面
中,侧面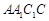
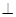 底面ABC,底面ABC是边长为2的等边三角形,侧面
底面ABC,底面ABC是边长为2的等边三角形,侧面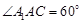 ,E、F分别是
,E、F分别是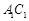 、AB的中点.
、AB的中点.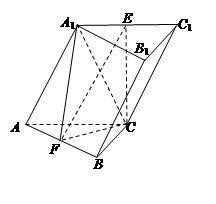
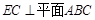 ;
;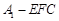 的体积.
的体积.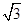 ,则棱锥O-ABCD的体积为________.
,则棱锥O-ABCD的体积为________.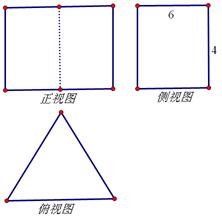
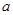 升水.平放在地面,则水面正好过圆锥的顶点
升水.平放在地面,则水面正好过圆锥的顶点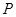 ,若将容器倒置如图2,水面也恰过点
,若将容器倒置如图2,水面也恰过点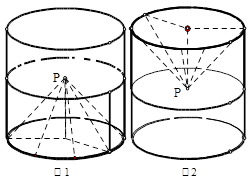
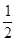 ;
;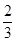 ;
;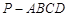 中,底面
中,底面 是边长为
是边长为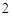 的菱形,
的菱形,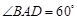 ,侧棱
,侧棱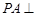 底面
底面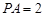 ,
,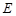 为
为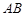 的中点,则四面体
的中点,则四面体 的体积为 .
的体积为 .