题目内容
已知双曲线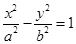 的一条渐近线方程为
的一条渐近线方程为 ,则其离心率为 。
,则其离心率为 。
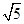
解析试题分析:根据题意可知,双曲线的焦点在x轴上,则可知其渐近线方程为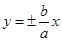 ,由于给定的渐近线斜率为2,则可知
,由于给定的渐近线斜率为2,则可知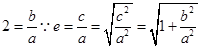 ,则可知e=
,则可知e=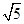 ,故答案为
,故答案为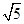 。
。
考点:本试题考查了双曲线的性质运用。
点评:解决该试题的关键是理解双曲线的渐近线方程的表示得到参数a,b的比值,进而利用a,b,c的三者的关系得到a,c的比值,进而得到离心率,属于基础题。

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
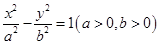 的左右顶点分别是
的左右顶点分别是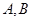 ,点
,点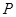 是双曲线上异于点
是双曲线上异于点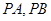 的斜率之积等于2,则该双曲线的离心率等于
的斜率之积等于2,则该双曲线的离心率等于  恰有一个公共点,则k的取值范围是___________
恰有一个公共点,则k的取值范围是___________ 的渐近线方程为 .
的渐近线方程为 .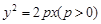 的焦点在圆
的焦点在圆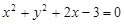 上,则
上,则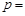 .
. 上,则这个三角形的面积为 。
上,则这个三角形的面积为 。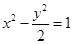 上两点,O为坐标原点.若
上两点,O为坐标原点.若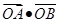 =0,则ΔAOB面积的最小值为______
=0,则ΔAOB面积的最小值为______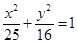 上的三点,点F(3,0),若
上的三点,点F(3,0),若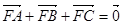 ,则
,则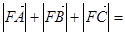
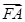 +
+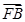 +
+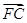 =0,则|
=0,则|