题目内容
已知x＞4，函数y=-x+
，当x=______时，函数有最______值是______．
| 1 |
| 4-x |
∵y=-x+
，
∴-y=x+
=（x-4）+
+4
∵x＞4?x-4＞0
∴（x-4）+
≥2
=2，
当且仅当x-4=
，即x=5时等号成立
所以-y=x+
=（x-4）+
+4≥2+4=6
可得y≤-6，当仅且当x=5时，y的最大值为-6
故答案为：5，大，-6．
| 1 |
| 4-x |
∴-y=x+
| 1 |
| x-4 |
| 1 |
| x-4 |
∵x＞4?x-4＞0
∴（x-4）+
| 1 |
| x-4 |
(x-4)•
|
当且仅当x-4=
| 1 |
| x-4 |
所以-y=x+
| 1 |
| x-4 |
| 1 |
| x-4 |
可得y≤-6，当仅且当x=5时，y的最大值为-6
故答案为：5，大，-6．
练习册系列答案
名校课堂系列答案
相关题目
，则当x＝________时，函数有最________值是________．
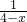，当x=________时，函数有最________值是________．
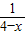，当x= 时，函数有最 值是 ．