题目内容
已知x＞4，函数y=-x+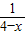
，当x= 时，函数有最 值是 ．
【答案】分析：根据函数的形式进行配凑，得到-y=（x-4）+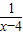
+4，再根据x-4＞0，运用基本不等式，得到右边当x=5时具有最小值6，最后用不等式的基本性质变形得到y≤-6，当仅且当x=5时，y的最大值为-6．
解答：解：∵y=-x+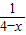
，
∴-y=x+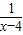
=（x-4）+
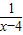+4
∵x＞4⇒x-4＞0
∴（x-4）+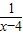
≥
，
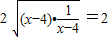当且仅当x-4=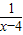
，即x=5时等号成立
所以-y=x+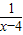
=（x-4）+
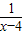+4≥2+4=6
可得y≤-6，当仅且当x=5时，y的最大值为-6
故答案为：5，大，-6．
点评：本题以分式函数求最值为例，考查了基本不等式的应用，属于基础题．再运用基本不等式的同时，应该注意各项为正数和取等号的条件以免出错．
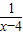+4，再根据x-4＞0，运用基本不等式，得到右边当x=5时具有最小值6，最后用不等式的基本性质变形得到y≤-6，当仅且当x=5时，y的最大值为-6．解答：解：∵y=-x+
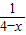，∴-y=x+
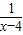=（x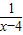-4）++4∵x＞4⇒x-4＞0
∴（x-4）+
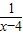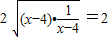≥，当且仅当x-4=
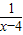，即x=5时等号成立所以-y=x+
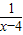=（x-4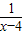）++4≥2+4=6可得y≤-6，当仅且当x=5时，y的最大值为-6
故答案为：5，大，-6．
点评：本题以分式函数求最值为例，考查了基本不等式的应用，属于基础题．再运用基本不等式的同时，应该注意各项为正数和取等号的条件以免出错．
练习册系列答案
相关题目
，则当x＝________时，函数有最________值是________．
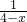，当x=________时，函数有最________值是________．