Question

已知集合M是同时满足下列两个性质的函数f（x）的全体：
①f（x）在其定义域上是单调增函数或单调减函数；
②在f（x）的定义域内存在区间[a，b]，使得f（x）在[a，b]上的值域是[

1

2

a，

1

2

b]．
（Ⅰ）判断函数y=-x³是否属于集合M？并说明理由．若是，请找出区间[a，b]；
（Ⅱ）若函数y=

x-1

+t∈M，求实数t的取值范围．

Answer 1

分析：（Ⅰ）判断函数y=-x³是否属于集合M即检验函数y=-x³是否满足①②，①可利用导数判单调性，②即判断

-b3= 1 2 a -a3= 1 2 b

是否有解．
（Ⅱ）若函数y=

x-1

+t∈M，可判断g（x）是定义域[1，+∞）上的增函数，故g（x）满足②即方程g(x)=

1

2

x在[1，+∞）内有两个不等实根，方法一：平方去根号，转化为二次函数在特定区间上解的问题，利用实根分布处理；方法二：可转化为方程

x-1

=

1

2

x-t在[1，+∞）内有两个不等实根，两个函数的图象有两个交点．结合图象求解．两种方法中都要注意等价转化．

解答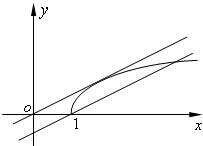：解：（Ⅰ）y=-x³的定义域是R，
∵y′=-3x²≤0，∴y=-x³在R上是单调减函数．
则y=-x³在[a，b]上的值域是[-b³，-a³]．
由

-b3= 1 2 a -a3= 1 2 b.

解得：

a=- 2 2 b= 2 2 .

或

a= 2 2 b=- 2 2 .

（舍去）或

a=0 b=0.

（舍去）
∴函数y=-x³属于集合M，且这个区间是[-

2

2

，

2

2

]．

（Ⅱ）设g(x)=

x-1

+t，则易知g（x）是定义域[1，+∞）上的增函数．
∵g（x）∈M，∴存在区间[a，b]?[1，+∞），满足g(a)=

1

2

a，g(b)=

1

2

b．
即方程g(x)=

1

2

x在[1，+∞）内有两个不等实根．
[法一]：方程

x-1

+t=

1

2

x在[1，+∞）内有两个不等实根，
等价于方程x-1=(

1

2

x-t)2在[2t，+∞）内有两个不等实根．
即方程x²-（4t+4）x+4t²+4=0在[2t，+∞）内有两个不等实根．
根据一元二次方程根的分布有

(2t)2-(4t+4)•2t+4t2+4≥0 △=(4t+4)2-4(4t2+4)＞0 4t+4 2 ＞2t.

解得0＜t≤

1

2

．
因此，实数t的取值范围是0＜t≤

1

2

．
[法二]：要使方程

x-1

+t=

1

2

x在[1，+∞）内有两个不等实根，
即使方程

x-1

=

1

2

x-t在[1，+∞）内有两个不等实根．
如图，当直线y=

1

2

x-t经过点（1，0）时，t=

1

2

，

当直线y=

1

2

x-t与曲线y=

x-1

相切时，
方程

x-1

=

1

2

x-t两边平方，得x²-（4t+4）x+4t²+4=0，由△=0，得t=0．
因此，利用数形结合得实数t的取值范围是0＜t≤

1

2

．

点评：本题考查集合的包含关系、函数的定义域、值域问题，同时考查数形结合思想、等价转化思想和利用所学知识分析问题、解决问题的能力．