题目内容
已知椭圆C的焦点为F1(-1,0)、F2(1,0),点P(-1,
)在椭圆上.
(1)求椭圆C的方程;
(2)若抛物线y2=2px(p>0)与椭圆C相交于点M、N,当△OMN(O是坐标原点)的面积取得最大值时,求p的值.
| ||
| 2 |
(1)求椭圆C的方程;
(2)若抛物线y2=2px(p>0)与椭圆C相交于点M、N,当△OMN(O是坐标原点)的面积取得最大值时,求p的值.
分析:(1)利用椭圆的定义及参数a,b,c的关系即可得出;
(2)利用椭圆和抛物线的对称性,可设出点P的坐标,进而表示出三角形的面积,利用基本不等式的性质及点在椭圆上即可得出.
(2)利用椭圆和抛物线的对称性,可设出点P的坐标,进而表示出三角形的面积,利用基本不等式的性质及点在椭圆上即可得出.
解答:解:(1)依题意,设椭圆C的方程为
+
=1,
∵2a=|PF1|+|PF2|=
+
=2
,∴a=
,c=1,∴b=
=1,
∴椭圆C的方程为
+y2=1.
(2)根据椭圆和抛物线的对称性,设M(x0,y0)、N(x0,-y0)(x0,y0>0),
△OMN的面积S=
x0×(2y0)=x0y0,
∵M(x0,y0)在椭圆上,∴
+y02=1,
∴1=
+y02≥2
=
x0y0,等号当且仅当
=y0时成立,
解
(x0,y0>0)得
,M(x0,y0)即M(1,
).
∵点M在抛物线y2=2px上,∴(
)2=2p×1,解得p=
.
∴p=
.
| x2 |
| a2 |
| y2 |
| b2 |
∵2a=|PF1|+|PF2|=
0+(
|
22+(
|
| 2 |
| 2 |
| a2-c2 |
∴椭圆C的方程为
| x2 |
| 2 |
(2)根据椭圆和抛物线的对称性,设M(x0,y0)、N(x0,-y0)(x0,y0>0),
△OMN的面积S=
| 1 |
| 2 |
∵M(x0,y0)在椭圆上,∴
| x02 |
| 2 |
∴1=
| x02 |
| 2 |
|
| 2 |
| x0 | ||
|
解
|
|
| ||
| 2 |
∵点M在抛物线y2=2px上,∴(
| ||
| 2 |
| 1 |
| 4 |
∴p=
| 1 |
| 4 |
点评:熟练正确圆锥曲线的定义及其性质、基本不等式的性质是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
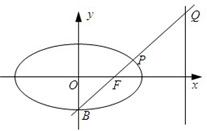 如图,已知椭圆C的方程为:
如图,已知椭圆C的方程为: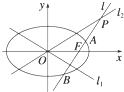 已知椭圆C的方程为
已知椭圆C的方程为