题目内容
已知椭圆C的对称轴为坐标轴,一个焦点为F(0,-
),点M(1,
)在椭圆C上
(Ⅰ)求椭圆C的标准方程
(Ⅱ)已知直线l:2x-y-2=0与椭圆C交于A,B两点,求△MAB的面积
(Ⅲ)设P为椭圆C上一点,若∠PMF=90°,求P点的坐标.
| 2 |
| 2 |
(Ⅰ)求椭圆C的标准方程
(Ⅱ)已知直线l:2x-y-2=0与椭圆C交于A,B两点,求△MAB的面积
(Ⅲ)设P为椭圆C上一点,若∠PMF=90°,求P点的坐标.
分析:(Ⅰ)椭圆C的对称轴为坐标轴,一个焦点为F(0,-
),故可设椭圆C的方程为
+
=1,再将点M的坐标代入即可的a2的值,最后写出标准方程即可
(Ⅱ)先将直线l与椭圆C的方程联立,解得A、B两点的坐标,从而求出|AB|,再利用点到直线的距离公式,计算M到直线AB的距离d,最后由三角形面积公式S△MAB=
|AB|•d计算△MAB的面积即可
(Ⅲ)先由∠PMF=90°得直线PM的斜率,从而写出直线PM的方程,再代入椭圆的方程,即可解得P点的坐标,注意此直线与椭圆有两个交点M,P
| 2 |
| y2 |
| a2 |
| x2 |
| a2-2 |
(Ⅱ)先将直线l与椭圆C的方程联立,解得A、B两点的坐标,从而求出|AB|,再利用点到直线的距离公式,计算M到直线AB的距离d,最后由三角形面积公式S△MAB=
| 1 |
| 2 |
(Ⅲ)先由∠PMF=90°得直线PM的斜率,从而写出直线PM的方程,再代入椭圆的方程,即可解得P点的坐标,注意此直线与椭圆有两个交点M,P
解答:解:(Ⅰ)∵椭圆C的对称轴为坐标轴,一个焦点为F(0,-
),
可设椭圆C的方程为
+
=1
将点M(1,
)代入方程得
+
=1
解得a2=4或a2=1(舍去)
∴椭圆C的标准方程为
+
=1
(Ⅱ)联立直线l与椭圆C的方程
解得
,
即A(0,-2),B(
,
)
∴|AB|=
=
点M(1,
)到直线l的距离d=
=
∴S△MAB=
|AB|•d=
×
×
=
(Ⅲ)设直线FM的斜率为k,则k=
=2
∵直线PM垂直于直线FM
∵直线PM的斜率为-
=-
故直线PM的方程为y=-
(x-5)
代入椭圆方程得17x2-10x-7=0,解得x=1或x=-
∴点P的坐标为(-
,
)
| 2 |
可设椭圆C的方程为
| y2 |
| a2 |
| x2 |
| a2-2 |
将点M(1,
| 2 |
| 2 |
| a2 |
| 1 |
| a2-2 |
解得a2=4或a2=1(舍去)
∴椭圆C的标准方程为
| y2 |
| 4 |
| x2 |
| 2 |
(Ⅱ)联立直线l与椭圆C的方程
|
解得
|
|
| 4 |
| 3 |
| 2 |
| 3 |
∴|AB|=
(
|
4
| ||
| 3 |
点M(1,
| 2 |
|2-
| ||
|
| ||
| 5 |
∴S△MAB=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
| ||
| 5 |
2
| ||
| 3 |
(Ⅲ)设直线FM的斜率为k,则k=
| ||||
| 1-0 |
| 2 |
∵直线PM垂直于直线FM
∵直线PM的斜率为-
| 1 |
| k |
| ||
| 4 |
故直线PM的方程为y=-
| ||
| 4 |
代入椭圆方程得17x2-10x-7=0,解得x=1或x=-
| 7 |
| 17 |
∴点P的坐标为(-
| 7 |
| 17 |
23
| ||
| 17 |
点评:本题考察了椭圆的标准方程及其求法,直线与椭圆的位置关系,特别是直线与椭圆相交时如何求弦长和三角形面积.

练习册系列答案
相关题目
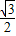 .
.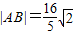 ,求直线l的方程.
,求直线l的方程.