题目内容
已知椭圆C的中心为原点,点F(1,0)是它的一个焦点,直线l过点F与椭圆C交于A,B两点,且当直线l垂直于x轴时,OA•OB=| 5 | 6 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在直线l,使得在椭圆C的右准线上可以找到一点P,满足△ABP为正三角形.如果存在,求出直线l的方程;如果不存在,请说明理由.
分析:(1)由题意,由于告诉了椭圆为焦点在x轴的椭圆所以可以利用定义设出 方程,然后建立a,b的方程求解即可;
(2)问是否存在的问题在圆锥曲线中就先假设存在,分斜率存在于不存在加以讨论,并把直线方程与椭圆方程进行连联立,利用设而不求整体代换进行求解.
(2)问是否存在的问题在圆锥曲线中就先假设存在,分斜率存在于不存在加以讨论,并把直线方程与椭圆方程进行连联立,利用设而不求整体代换进行求解.
解答:解:(Ⅰ)设椭圆C的方程为:
+
=1(a>b>0),则a2-b2=1.①
∵当l垂直于x轴时,A,B两点坐标分别是(1,
)和(1,-
),
∴
•
=(1,
)•(1,-
)=1-
,则1-
=
,即a2=6b4.②
由①,②消去a,得6b4-b2-1=0.∴b2=
或b2=-
.
当b2=
时,a2=
.因此,椭圆C的方程为
+2y2=1.
(Ⅱ)设存在满足条件的直线l.
(1)当直线l垂直于x轴时,由(Ⅰ)的解答可知|AB|=
=
,焦点F到右准线的距离为d=
-c=
,
此时不满足d=
|AB|.
因此,当直线l垂直于x轴时不满足条件.
(2)当直线l不垂直于x轴时,设直线l的斜率为k,则直线l的方程为y=k(x-1).
由
?(6k2+2)x2-12k2x+6k2-3=0,
设A,B两点的坐标分别为(x1,y1)和(x2,y2),则x1+x2=
,x1x2=
.
|AB|=
|x1-x2|=
=
=-
.
又设AB的中点为M,则xM=
=
.
当△ABP为正三角形时,直线MP的斜率为kMP=-
.
∵xp=
,∴|MP|=
|xp-xM|=
•(
-
)=
•
.
当△ABP为正三角形时,|MP|=
|AB|,即
•
=
•
,
解得k2=1,k=±1.
因此,满足条件的直线l存在,且直线l的方程为x-y-1=0或x+y-1=0.
| x2 |
| a2 |
| y2 |
| b2 |
∵当l垂直于x轴时,A,B两点坐标分别是(1,
| b2 |
| a |
| b2 |
| a |
∴
| OA |
| OB |
| b2 |
| a |
| b2 |
| a |
| b4 |
| a2 |
| b4 |
| a2 |
| 5 |
| 6 |
由①,②消去a,得6b4-b2-1=0.∴b2=
| 1 |
| 2 |
| 1 |
| 3 |
当b2=
| 1 |
| 2 |
| 3 |
| 2 |
| 2x2 |
| 3 |
(Ⅱ)设存在满足条件的直线l.
(1)当直线l垂直于x轴时,由(Ⅰ)的解答可知|AB|=
| 2b2 |
| a |
| ||
| 3 |
| a2 |
| c |
| 1 |
| 2 |
此时不满足d=
| ||
| 2 |
因此,当直线l垂直于x轴时不满足条件.
(2)当直线l不垂直于x轴时,设直线l的斜率为k,则直线l的方程为y=k(x-1).
由
|
设A,B两点的坐标分别为(x1,y1)和(x2,y2),则x1+x2=
| 6k2 |
| 3k2+1 |
| 6k2-3 |
| 6k2+2 |
|AB|=
| 1+k2 |
| (1+k2)[(x1+x2) 2-4x1x2] |
(1+k2)[(
|
| ||
| 3k2+1 |
又设AB的中点为M,则xM=
| x1+x2 |
| 2 |
| 3k2 |
| 3k2+1 |
当△ABP为正三角形时,直线MP的斜率为kMP=-
| 1 |
| k |
∵xp=
| 3 |
| 2 |
1+
|
1+
|
| 3 |
| 2 |
| 3k2 |
| 3k2+1 |
|
| 3(k2+1) |
| 2(3k2+1) |
当△ABP为正三角形时,|MP|=
| ||
| 2 |
|
| 3(k2+1) |
| 2(3k2+1) |
| ||
| 2 |
| ||
| 3k2+1 |
解得k2=1,k=±1.
因此,满足条件的直线l存在,且直线l的方程为x-y-1=0或x+y-1=0.
点评:(1)次问重点考查了利用方程的思想由题意列出变量a,b的两个方程,然后求解曲线的轨迹方程;
(2)次问重点考查了分类讨论的思想及把直线方程与圆锥曲线方程进行联立设而不求整体代换的思想,还有对于圆锥曲线中是否存在利用假设的解题方法.
(2)次问重点考查了分类讨论的思想及把直线方程与圆锥曲线方程进行联立设而不求整体代换的思想,还有对于圆锥曲线中是否存在利用假设的解题方法.

练习册系列答案
相关题目
 (2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
(2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为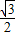 ,且点
,且点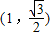 在该椭圆上.
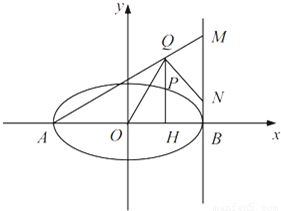
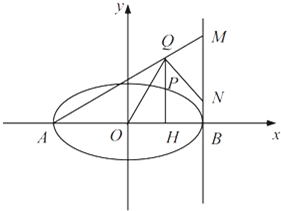
在该椭圆上.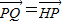 ,直线AQ与过点B 且垂直于x 轴的直线交于点M,
,直线AQ与过点B 且垂直于x 轴的直线交于点M,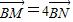 .求证:∠OQN为锐角.
.求证:∠OQN为锐角.