题目内容
有一种舞台灯,外形是正六棱柱,在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用 表示更换的面数,用
表示更换的面数,用 表示更换费用。
表示更换费用。
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出 的分布列,求
的分布列,求 的数学期望。
的数学期望。
 表示更换的面数,用
表示更换的面数,用 表示更换费用。
表示更换费用。(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出
 的分布列,求
的分布列,求 的数学期望。
的数学期望。(1) 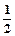 (2)
(2)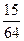 (3)
(3)
E =300
=300
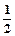 (2)
(2)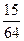 (3)
(3) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 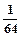 | 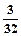 | 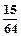 | 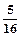 | 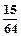 | 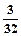 | 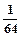 |
 =300
=300 (1)因为①号面不需要更换的概率为: 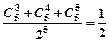
所以①号面需要更换的概率为:P=1-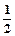 =
=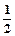
(2)根据独立重复试验,6个面中恰好有2个面需要更换的概率为:
P6(2)=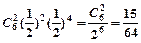
(3)因为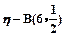 ,又P6(0)=
,又P6(0)=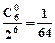 ,P6(1)=
,P6(1)= 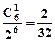 ,P6(2)=
,P6(2)= 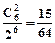 ,P6(3)=
,P6(3)= 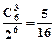 ,P6(4)=
,P6(4)= 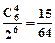 ,P6(5)=
,P6(5)= 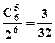 ,P6(6)=
,P6(6)= 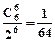
 的分布列为:
的分布列为:
 =100
=100 ,E
,E =100E
=100E =300
=300
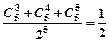
所以①号面需要更换的概率为:P=1-
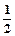 =
=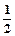
(2)根据独立重复试验,6个面中恰好有2个面需要更换的概率为:
P6(2)=
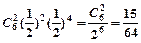
(3)因为
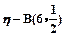 ,又P6(0)=
,又P6(0)=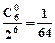 ,P6(1)=
,P6(1)= 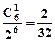 ,P6(2)=
,P6(2)= 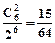 ,P6(3)=
,P6(3)= 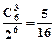 ,P6(4)=
,P6(4)= 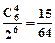 ,P6(5)=
,P6(5)= 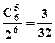 ,P6(6)=
,P6(6)= 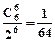
 的分布列为:
的分布列为: | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 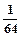 | 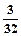 | 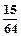 | 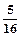 | 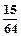 | 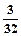 | 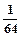 |
 =100
=100 ,E
,E =100E
=100E =300
=300
练习册系列答案
相关题目
 校高三年级学生家庭月平均收入不多于10000元的共有100
校高三年级学生家庭月平均收入不多于10000元的共有100 0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示.
0人,统计这些学生家庭月平均收入情况,得到家庭月平均收入频率分布直方图如图所示. (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在 (元)间的同学不发助学金.
(元)间的同学不发助学金.
 元,写出
元,写出 元,求
元,求 .
. 的分布列为
的分布列为



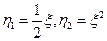 的分布列.
的分布列. 个,在小球上分别标有1,2,3,
个,在小球上分别标有1,2,3, ,
, ,
, (如取2468时,
(如取2468时, 的值;(ⅱ)求随机变量
的值;(ⅱ)求随机变量 布列及均值.
布列及均值. .
. 的分布列为
的分布列为 ……
…… ,且
,且 ,则
,则 的值为
的值为 