题目内容
【题目】已知数列{an}，an=（2n+m）+（﹣1）n（3n﹣2）（m∈N* ， m与n无关），若 
a2i﹣1≤k2﹣2k﹣1对一切m∈N*恒成立，则实数k的取值范围为 ．
【答案】（﹣∞，﹣1]∪[3，+∞）
【解析】解：a2i﹣1=2（2i﹣1）+m+（﹣1）2i﹣1[3（2i﹣1）﹣2]=4i﹣2+m﹣（6i﹣5）=﹣2i+m+3， 
a2i﹣1= （﹣2i+m+3）=﹣2 i+2m（m+3）= 
+2m2+6m=﹣2m2+4m，
∴﹣2m2+4m≤k2﹣2k﹣1恒成立，
∵﹣2m2+4m=﹣2（m﹣1）2+2≤2，
∴k2﹣2k﹣1≥2恒成立，即k2﹣2k﹣3≥0，
解得k≥3或k≤﹣1．
所以答案是（﹣∞，﹣1]∪[3，+∞）．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系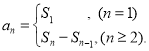
．
练习册系列答案
相关题目
【题目】某汽车美容公司为吸引顾客，推出优惠活动：对首次消费的顾客，按200元/次收费，并注册成为会员，对会员逐次消费给予相应优惠，标准如表：
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
该公司从注册的会员中，随机抽取了100位进行统计，得到统计数据如表：
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
频数 | 60 | 20 | 10 | 5 | 5 |
假设汽车美容一次，公司成本为150元，根据所给数据，解答下列问题：
（1）估计该公司一位会员至少消费两次的概率；
（2）某会员仅消费两次，求这两次消费中，公司获得的平均利润；
（3）设该公司从至少消费两次，求这的顾客消费次数用分层抽样方法抽出8人，再从这8人中抽出2人发放纪念品，求抽出2人中恰有1人消费两次的概率．
