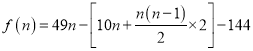��Ŀ����
����Ŀ��ij���佫![]() ������ƽ���ֳɼס�������ӹ�ij��������ڵ�λʱ����ÿ�������ӹ��ĺϸ�������ľ�Ҷͼ��ͼ����֪���鼼���ڵ�λʱ���ڼӹ��ĺϸ������ƽ������Ϊ
������ƽ���ֳɼס�������ӹ�ij��������ڵ�λʱ����ÿ�������ӹ��ĺϸ�������ľ�Ҷͼ��ͼ����֪���鼼���ڵ�λʱ���ڼӹ��ĺϸ������ƽ������Ϊ![]() .
.

��1����![]() ��
��![]() ��ֵ��
��ֵ��
��2����ס������鼼���ڵ�λʱ���ڼӹ��ĺϸ�����ķ���![]() ��
��![]() �����ɴ˷������鼼���ļӹ�ˮƽ��
�����ɴ˷������鼼���ļӹ�ˮƽ��
��3���ʼ첿�ŴӸó���ס������鼼���и������ȡһ��������ӹ���������м�⣬�����˼ӹ��ĺϸ��������֮�ʹ���![]() ����Ƹó��䡰�����ϸ���ó��䡰�����ϸĸ���.
����Ƹó��䡰�����ϸ���ó��䡰�����ϸĸ���.
��������![]() ������
������![]() ����
Ϊ����![]() ��ƽ����
��ƽ����
���𰸡���1��3,8����2��������ȶ�һЩ����3��![]() .
.
����������������1�������鼼���ڵ�λʱ���ڼӹ��ĺϸ������ƽ������Ϊ![]() �����þ�Ҷͼ�����
�����þ�Ҷͼ�����![]() ��
��![]() ��ֵ��
��ֵ��
��2���ȷֱ����![]() ��
��![]() �������鼼���ڵ�λʱ���ڼӹ��ĺϸ������ƽ������Ϊ
�������鼼���ڵ�λʱ���ڼӹ��ĺϸ������ƽ������Ϊ![]() ��
��![]() ���õ�������ȶ�һЩ��
���õ�������ȶ�һЩ��
��3���ʼ첿�ŴӸó���ס������鼼���и������ȡһ��������ӹ���������м�⣬�����˼ӹ��ĺϸ�������ֱ�Ϊ![]() ��
��![]() �������оٷ�������ó��䡰�����ϸĸ���.
�������оٷ�������ó��䡰�����ϸĸ���.
��⣺��1�����������֪��![]() ��
��
![]() ��
��
���![]() ��
��![]() .
.
��2��![]() ��
��
![]() ��
��
��![]() ��
��![]() ��
��
��ס������������ˮƽ�൱��������ȶ�һЩ.
��3���ʼ첿�ŴӸó���ס������鼼���и������ȡһ��������ӹ���������м�⣬�����˼ӹ��ĺϸ�������ֱ�Ϊ![]() ��
��![]() ��������
��������![]() �Ŀ���Ϊ
�Ŀ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ��.
��.
��![]() �Ļ����¼���
�Ļ����¼���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������
������![]() ����
����
������![]() �Ļ����¼�����
�Ļ����¼�����![]() ��������
��������
�ʸó��䡰�����ϸĸ���Ϊ![]() .
.