题目内容
【题目】设函数![]() .
.
(1)若![]() 时,
时,![]() 取得极值,求
取得极值,求![]() 的值;
的值;
(2)若![]() 在其定义域内为增函数,求
在其定义域内为增函数,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)先求函数的导函数,根据若![]() 时,
时,![]() 取得极值得
取得极值得![]() ,解之即可;(2)
,解之即可;(2)![]() 在其定义域内为增函数可转化成只需在
在其定义域内为增函数可转化成只需在![]() 内有
内有![]() 恒成立,根据二次函数的图象与性质建立不等式关系,解之即可.
恒成立,根据二次函数的图象与性质建立不等式关系,解之即可.
试题解析:![]()
(1)因为![]() 时,
时,![]() 取得极值,所以
取得极值,所以![]() ,
,
即![]() 故
故![]() .
.
(2)![]() 的定义域为
的定义域为![]() .方程
.方程![]() 的判别式
的判别式![]() ,
,
(Ⅰ) 当![]() , 即
, 即![]() 时,
时,![]() ,
,
![]() 在
在![]() 内恒成立, 此时
内恒成立, 此时![]() 为增函数.
为增函数.
(Ⅱ)当![]() , 即
, 即![]() 或
或![]() 时,
时,
要使![]() 在定义域
在定义域![]() 内为增函数, 只需在
内为增函数, 只需在![]() 内有
内有![]() 即可,
即可,
设![]() ,
,
由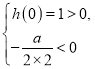 得
得 ![]() , 所以
, 所以![]() .
.
由(1) (2)可知,若![]() 在其定义域内为增函数,
在其定义域内为增函数,![]() 的取值范围是
的取值范围是![]() .
.
【方法点晴】本题主要考查利用导数研究函数的极值以及利用单调性求参数的范围,属于中档题. 利用单调性求参数的范围的常见方法:① 视参数为已知数,依据函数的图象或单调性定义,确定函数的单调区间,与已知单调区间比较求参数需注意若函数在区间![]() 上是单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式
上是单调的,则该函数在此区间的任意子集上也是单调的; ② 利用导数转化为不等式![]() 或
或![]() 恒成立问题求参数范围,本题(2)是利用方法 ② 求解的.
恒成立问题求参数范围,本题(2)是利用方法 ② 求解的.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】为了调查某大学学生在某天上网的时间,随机对100名男生和100名女生进行了不记名的问卷调查. 得到如下的统计结果.
表1:男生上网时间与频数分布表:
上网时间(分钟) |
|
|
|
|
|
人数 | 10 | 20 | 40 | 20 | 10 |
表2:女生上网时间与频数分布表:
上网时间(分钟) |
|
|
|
|
|
人数 | 5 | 25 | 30 | 25 | 15 |
完成下面的2×2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?


附: ,其中
,其中![]()