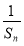Question

在正项数列{an}中，a1＝2，an＋1＝2an＋3×5n，则数列{an}的通项公式为________．

 

Answer 1

an＝5n－3×2n－1

【解析】在递推公式an＋1＝2an＋3×5n的两边同时除以5n＋1，得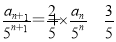，①

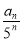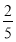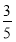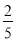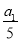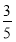令＝bn，则①式变为bn＋1＝bn＋，即bn＋1－1＝(bn－1)，所以数列{bn－1}是等比数列，其首项为b1－1＝－1＝－，公比为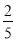所以bn－1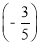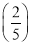＝×n－1，即b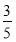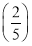n＝1－×n－1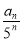＝，故an＝5n－3×2n－1.