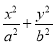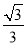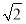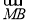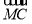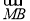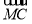题目内容
已知首项为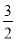
的等比数列{an}不是递减数列，其前n项和为Sn(n∈N*)，且S3＋a3，S5＋a5，S4＋a4成等差数列．
(1)求数列{an}的通项公式；
(2)设Tn＝Sn－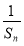
(n∈N*)，求数列{Tn}的最大项的值与最小项的值．
（1）(－1)n－1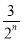
（2）
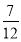
【解析】(1)解 设等比数列{an}的公比为q，因为S3＋a3，S5＋a5，S4＋a4成等差数列，所以S5＋a5－S3－a3＝S4＋a4－S5－a5，即4a5＝a3，于是q2＝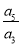
＝
.
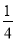又{an}不是递减数列且a1＝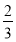
，所以q＝－
.
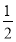故等比数列{an}的通项公式为
an＝×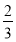
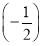n－1＝(－1)n－1.
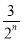(2)由(1)得Sn＝1－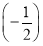
n＝
，当n为奇数时，Sn随n的增大而减小，所以1<Sn≤S1＝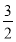
，故0<Sn－
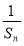≤S1－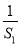
＝
－＝
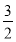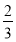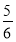
当n为偶数时，Sn随n的增大而增大，所以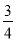
＝S2≤Sn<1，故0>Sn－
≥S2－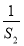
＝－
＝－
.
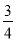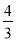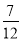综上，对于n∈N*，总有－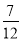
≤Sn－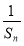
≤
.
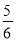所以数列{Tn}最大项的值为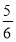
，
最小项的值为－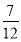
.
练习册系列答案
相关题目
随机询问100名性别不同的大学生是否爱好踢毽子运动，得到如下的列联表：
| 男 | 女 | 总计 |
爱好 | 10 | 40 | 50 |
不爱好 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
附表：
P(K2≥k0) | 0.10 | 0.05 | 0.025 |
k0 | 2.706 | 3.841 | 5.024 |
经计算，统计量K2＝4.762，参照附表，得到的正确结论是( )．
A．在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关”
B．在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关”
C．有97.5%以上的把握认为“爱好该项运动与性别有关”
D．有97.5%以上的把握认为“爱好该项运动与性别无关”
