题目内容
给定以下命题:(1)函数y=x+cosx在区间
 上有唯一的零点;
上有唯一的零点;(2)向量
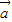 与向量
与向量 共线,则向量
共线,则向量 与向量
与向量 方向相同或是方向相反;
方向相同或是方向相反;(3)若角α=β,则一定有tanα=tanβ;
(4)若?x∈R,使f′(x)=0,则函数f(x)在x=x处取得极大或是极小值.
则上述命题中,假命题的个数为( )
A.4个
B.3个
C.2个
D.1个
【答案】分析:(1)对函数进行求导,研究函数的单调性,从而可判断函数y=x+cosx在区间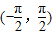 上有唯一的零点;
上有唯一的零点;
(2)当两个向量中有零向量时,结论不正确;(3)若角α=β= ,则tanα=tanβ不成立;
,则tanα=tanβ不成立;
(4)f′(x)=0,函数f(x)在x=x的左右附近,导数符号不改变时,结论不成立.
解答:解:(1)求导函数y′=1-sinx.∵x∈ ,∴y′>0,∴函数y=x+cosx在区间
,∴y′>0,∴函数y=x+cosx在区间 上单调增
上单调增
.∵x∈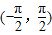 ,∴y∈
,∴y∈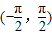 ,∴函数y=x+cosx在区间
,∴函数y=x+cosx在区间 上有唯一的零点,故(1)是真命题;
上有唯一的零点,故(1)是真命题;
(2)中未注意零向量,当两个向量中有零向量时,结论不正确,所以(2)为假命题,
(3)若角α=β=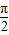 ,则tanα=tanβ不成立,故(3)为假命题;
,则tanα=tanβ不成立,故(3)为假命题;
(4)f′(x)=0,函数f(x)在x=x的左右附近,导数符号改变时,函数f(x)在x=x处取得极大或是极小值,否则不成立,故(4)为假命题.
综上知,(2)(3)(4)为假命题
故选B.
点评:本题主要考查函数的零点,函数的极值,考查向量知识,考查三角函数,注意结论成立的条件是关键.
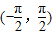 上有唯一的零点;
上有唯一的零点;(2)当两个向量中有零向量时,结论不正确;(3)若角α=β=
 ,则tanα=tanβ不成立;
,则tanα=tanβ不成立;(4)f′(x)=0,函数f(x)在x=x的左右附近,导数符号不改变时,结论不成立.
解答:解:(1)求导函数y′=1-sinx.∵x∈
 ,∴y′>0,∴函数y=x+cosx在区间
,∴y′>0,∴函数y=x+cosx在区间 上单调增
上单调增.∵x∈
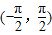 ,∴y∈
,∴y∈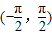 ,∴函数y=x+cosx在区间
,∴函数y=x+cosx在区间 上有唯一的零点,故(1)是真命题;
上有唯一的零点,故(1)是真命题;(2)中未注意零向量,当两个向量中有零向量时,结论不正确,所以(2)为假命题,
(3)若角α=β=
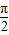 ,则tanα=tanβ不成立,故(3)为假命题;
,则tanα=tanβ不成立,故(3)为假命题;(4)f′(x)=0,函数f(x)在x=x的左右附近,导数符号改变时,函数f(x)在x=x处取得极大或是极小值,否则不成立,故(4)为假命题.
综上知,(2)(3)(4)为假命题
故选B.
点评:本题主要考查函数的零点,函数的极值,考查向量知识,考查三角函数,注意结论成立的条件是关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 与向量
与向量 共线,则向量
共线,则向量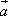 与向量
与向量 方向相同或是方向相反;
方向相同或是方向相反; 上有唯一的零点;
上有唯一的零点; 与向量
与向量 共线,则向量
共线,则向量