题目内容
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<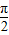 ),则四棱锥P-ABCD的体积V的取值范围是( )
),则四棱锥P-ABCD的体积V的取值范围是( )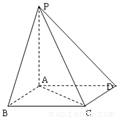
A.[
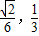 )
)B.(
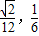 ]
]C.(
 ]
]D.[
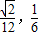 )
)
【答案】分析:先根据条件得到四边形ABCD的面积S=sinθ,由余弦定理可求得AC=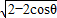 ,即可得到PA,进而表示出四棱锥P-ABCD的体积,整理后再借助于三角函数的取值范围即可解题.
,即可得到PA,进而表示出四棱锥P-ABCD的体积,整理后再借助于三角函数的取值范围即可解题.
解答:解:由已知,四边形ABCD的面积S=sinθ,
由余弦定理可求得AC=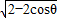 ,
,
∴PA=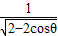 ,
,
∴V= •
•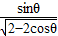
∴V=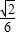 •
•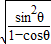 =
=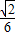 •
•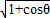
所以,当cosθ=0,即θ=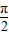 时,四棱锥V-ABCD的体积V的最小值是
时,四棱锥V-ABCD的体积V的最小值是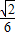
当cosθ=0,即θ=0时,四棱锥V-ABCD的体积V的最小值是
∵0<θ≤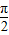
∴P-ABCD的体积V的取值范围是[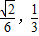 )
)
故选A
点评:本题主要考查棱锥的体积计算,熟练掌握余弦函数的图象和性质是解答的关键.
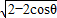 ,即可得到PA,进而表示出四棱锥P-ABCD的体积,整理后再借助于三角函数的取值范围即可解题.
,即可得到PA,进而表示出四棱锥P-ABCD的体积,整理后再借助于三角函数的取值范围即可解题.解答:解:由已知,四边形ABCD的面积S=sinθ,
由余弦定理可求得AC=
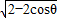 ,
,∴PA=
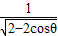 ,
,∴V=
 •
•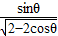
∴V=
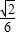 •
•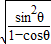 =
=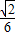 •
•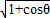
所以,当cosθ=0,即θ=
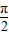 时,四棱锥V-ABCD的体积V的最小值是
时,四棱锥V-ABCD的体积V的最小值是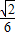
当cosθ=0,即θ=0时,四棱锥V-ABCD的体积V的最小值是

∵0<θ≤
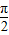
∴P-ABCD的体积V的取值范围是[
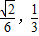 )
)故选A
点评:本题主要考查棱锥的体积计算,熟练掌握余弦函数的图象和性质是解答的关键.

练习册系列答案
相关题目
 如图,如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点.
如图,如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<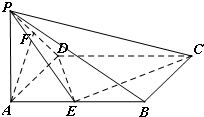 (2012•贵州模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,F是PD的中点,E是线段AB上的点.
(2012•贵州模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,F是PD的中点,E是线段AB上的点.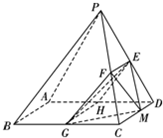 如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.