题目内容
 如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.(1)求证:AF∥平面PEC;
(2)设CD的中点为H,求证:平面EFH∥平面PBC;
(3)求AC与平面PCD所成的角的正弦值.
分析:(1)取PC中点M,连接FM,EM,根据线面平行的判定定理只需证明AF∥EM;
(2)根据面面平行的判定定理只需证明EH∥平面PBC,FH∥平面PBC,进而转化为证明EH∥BC,FH∥PC即可;
(3)先证明AF⊥平面PCD,连接FC,则∠ACF即为AC与平面PCD所成的角,在RT△ACF中,可求∠ACF的正弦值.
(2)根据面面平行的判定定理只需证明EH∥平面PBC,FH∥平面PBC,进而转化为证明EH∥BC,FH∥PC即可;
(3)先证明AF⊥平面PCD,连接FC,则∠ACF即为AC与平面PCD所成的角,在RT△ACF中,可求∠ACF的正弦值.
解答:解:(1)取PC中点M,连接FM,EM,
∵F、M分别为PD、PC的中点,∴FM∥DC,FM=
DC,
又E为AB的中点,∴AE∥DC,AE=
DC,
∴AE∥FM,AE=FM,∴四边形AFME为平行四边形,
∴AF∥ME,又AF?平面PEC,ME?平面PEC,
∴AF∥平面PEC.
(2)∵H为CD的中点,∴EH∥BC,又EH?平面PBC,BC?平面PBC,∴EH∥平面PBC.
∵F、H分别为PD、CD的中点,∴FH∥PC,又FH?平面PBC,PC?平面PBC,∴FH∥平面PBC.
又FH∩EH=H,FH?平面EFH,EH?平面EFH,
∴平面EFH∥平面PBC.
(3)∵PA=AD=1,F为PD的中点,∴AF⊥PD,
∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD,又CD⊥AD,PA∩AD=A,∴CD⊥平面PAD,
AF?平面PAD,∴CD⊥AF,又PD∩CD=D,∴AF⊥平面PCD,
连接FC,则∠ACF即为AC与平面PCD所成的角.
在等腰RT△PAD中,AF=
,在矩形ABCD中,AC=
=
,
∴在RT△AFC中,sin∠ACF=
=
=
.
∴AC与平面PCD所成的角的正弦值为
.
∵F、M分别为PD、PC的中点,∴FM∥DC,FM=
| 1 |
| 2 |
又E为AB的中点,∴AE∥DC,AE=
| 1 |
| 2 |
∴AE∥FM,AE=FM,∴四边形AFME为平行四边形,
∴AF∥ME,又AF?平面PEC,ME?平面PEC,
∴AF∥平面PEC.
(2)∵H为CD的中点,∴EH∥BC,又EH?平面PBC,BC?平面PBC,∴EH∥平面PBC.
∵F、H分别为PD、CD的中点,∴FH∥PC,又FH?平面PBC,PC?平面PBC,∴FH∥平面PBC.
又FH∩EH=H,FH?平面EFH,EH?平面EFH,
∴平面EFH∥平面PBC.
(3)∵PA=AD=1,F为PD的中点,∴AF⊥PD,
∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD,又CD⊥AD,PA∩AD=A,∴CD⊥平面PAD,
AF?平面PAD,∴CD⊥AF,又PD∩CD=D,∴AF⊥平面PCD,
连接FC,则∠ACF即为AC与平面PCD所成的角.
在等腰RT△PAD中,AF=
| ||
| 2 |
| 22+12 |
| 5 |
∴在RT△AFC中,sin∠ACF=
| AF |
| AC |
| ||||
|
| ||
| 10 |
∴AC与平面PCD所成的角的正弦值为
| ||
| 10 |
点评:本题考查线面平行、面面平行的判定及线面角的求解,考查学生的推理论证能力,解题关键是熟练掌握相关的定义、定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点.
如图,如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,E、F分别是AB、PD的中点. 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<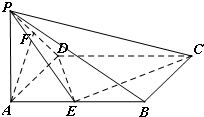 (2012•贵州模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,F是PD的中点,E是线段AB上的点.
(2012•贵州模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,F是PD的中点,E是线段AB上的点. 如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PD,PC,BC的中点.