Question

【题目】哈师大附中高三学年统计甲、乙两个班级一模数学分数（满分分），现有甲、乙两班本次考试数学分数如下列茎叶图所示：

（1）根据茎叶图求甲、乙两班同学成绩的中位数，并将以班同学的成绩的频率分布直方图填充完整；

（2）根据茎叶图比较在一模考试中，甲、乙两班同学数学成绩的平均水平和分数的分散程度（不要求计算出具体值，给出结论即可）；

（3）若规定分数在 的成绩为良好，分数在 的成绩为优秀，现从甲、乙两班成绩为优秀的同学中，按照各班成绩为优秀的同学人数占两班总的优秀人数的比例分层抽样，共选出 位同学参加数学提优培训，求这 位同学中恰含甲、乙两班所有 分以上的同学的概率.

Answer 1

【答案】(1)见解析;(2)见解析;(3).

【解析】分析：（1）直接根据中位数定义可得甲、乙两班同学成绩的中位数，根据频数求出频率，由频率除以组距可得纵坐标，从而可补全直方图；（2）乙班学生数学考试分数的平均水平高于甲班学生数学考试分数的平均水平；甲班学生数学考试分数的分散程度高于乙班学生数学考试分数的分散程度；（3）由分层抽样方法可得应从甲、乙两班各选出人、人，分别利用古典概型概率公式求出甲乙两班所有 分以上的同学被抽到的概率，利用独立事件概率公式可得结果.

详解：（1）甲班数学分数的中位数：

乙班数学分数的中位数：

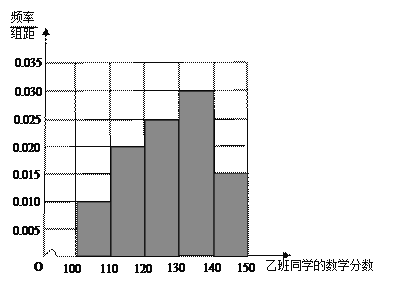
（2）乙班学生数学考试分数的平均水平高于甲班学生数学考试分数的平均水平；甲班学生数学考试分数的分散程度高于乙班学生数学考试分数的分散程度.

（3）有频率分布直方图可知：甲、乙两班数学成绩为优秀的人数分别为10、14， 若从中分层抽样选出12人，则应从甲、乙两班各选出5人、7人，设“选出的12人中恰含有甲、乙两班的所有140分以上的同学”为事件A

则

所以选出的12人中恰含有甲、乙两班的所有140分以上的同学的概率为.