题目内容
已知数列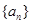 的前
的前 项和为
项和为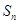 ,
,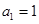 ,
, ,,则
,,则 。
。
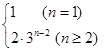
解析

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
设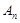 ,
,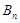 是等差数列
是等差数列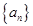 ,
,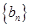 的前n项和,若
的前n项和,若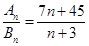 ,则使得
,则使得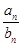 为整数的正整数n的个数是( ).
为整数的正整数n的个数是( ).
| A.2 | B.3 | C.4 | D.5 |
题目内容
已知数列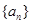 的前
的前 项和为
项和为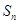 ,
,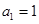 ,
, ,,则
,,则 。
。
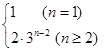
解析

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案设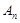 ,
,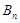 是等差数列
是等差数列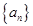 ,
,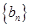 的前n项和,若
的前n项和,若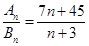 ,则使得
,则使得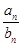 为整数的正整数n的个数是( ).
为整数的正整数n的个数是( ).
| A.2 | B.3 | C.4 | D.5 |