题目内容
已知数列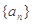 的前
的前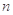 项和为
项和为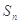 ,数列
,数列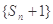 是公比为
是公比为 的等比数列,
的等比数列,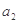 是
是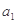 和
和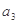 的等比中项.
的等比中项.
(1)求数列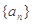 的通项公式;
的通项公式;
(2)求数列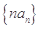 的前
的前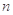 项和
项和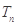 .
.
(1)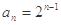 ;(2)
;(2) .
.
解析试题分析:
解题思路:(1)利用已知条件先求出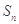 ,再求
,再求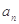 ;(2)用错位相减法求数列前n项和.
;(2)用错位相减法求数列前n项和.
规律总结:1求数列的通项公式一般有三种类型:①利用等差数列、等比数列的基本量求通项公式;②已知数列的首项与递推式,求通项公式;③利用 与
与 的关系求通项公式;
的关系求通项公式;
因为 是等差数列,
是等差数列,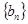 是等比数列,则求
是等比数列,则求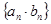 的和利用错位相减法.
的和利用错位相减法.
注意点:利用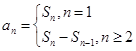 时,一定要验证
时,一定要验证 的式子是否满足
的式子是否满足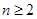 的表达式.
的表达式.
试题解析:(1)∵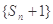 是公比为
是公比为 的等比数列,
的等比数列,
∴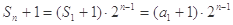 ,
,
∴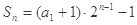 ,从而
,从而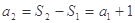 ,
,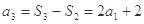 ,
,
∵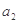 是
是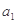 和
和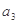 的等比中项∴
的等比中项∴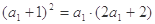 ,
,
解得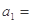
 或
或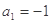 ,
,
当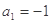 时,
时,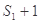
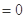 ,
,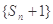 不是等比数列,
不是等比数列,
∴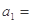
 .∴
.∴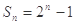 ,
,
当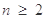 时,
时,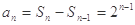 ,
,
∵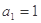 符合
符合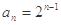 ,
,
∴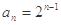 ;
;
(2)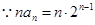 ,
,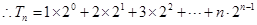 ,
,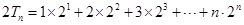 ,两式相减,得
,两式相减,得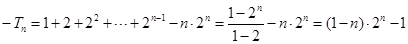 ,
, .
.
考点:1.已知 求
求 ;2.错位相减法.
;2.错位相减法.

练习册系列答案
相关题目
已知数列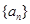 中,
中,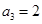 ,
,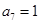 ,若
,若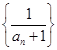 为等差数列,则
为等差数列,则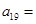 ( )
( )
A. | B.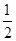 | C.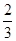 | D.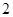 |
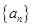 中,
中,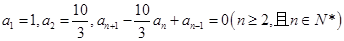
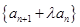 是等比数列, 求实数
是等比数列, 求实数 ;
;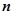 项和
项和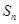 .
.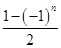 an-
an-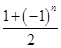 bn,求数列{cn}的前2n项和T2n.
bn,求数列{cn}的前2n项和T2n.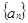 的前
的前 项和
项和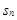 满足
满足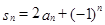 ,
,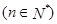
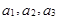
 ,求证:数列
,求证:数列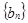 为等比数列,并指出
为等比数列,并指出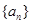 的前
的前 项和为
项和为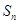 ,
,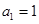 ,
, ,,则
,,则 。
。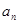 }中,
}中,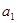 =
=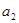 =1,
=1, 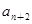 =
=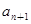 +
+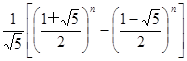 ,根据上述结论,可以知道不超过实数
,根据上述结论,可以知道不超过实数  的最大整数为
的最大整数为