题目内容
20．在边长为1的正三角形ABC中任取一点M，则AM＜$\frac{\sqrt{3}}{2}$的概率为（ ）| A． | $\frac{\sqrt{3}π}{18}$ | B． | $\frac{\sqrt{3}π}{12}$ | C． | $\frac{\sqrt{3}π}{9}$ | D． | $\frac{\sqrt{3}π}{6}$ |
分析 由题意可得三角形的面积和扇形的面积，由几何概型的概率公式可儿的．
解答 解：由题意该几何概型的总的基本事件的区域为边长为1的正三角形的面积S=$\frac{1}{2}×1×1×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$，
而满足AM＜$\frac{\sqrt{3}}{2}$的区域为扇形的面积S′=$\frac{1}{6}×π×（\frac{\sqrt{3}}{2}）^{2}$=$\frac{π}{8}$，
∴所求概率P=$\frac{S′}{S}$=$\frac{\sqrt{3}π}{6}$
故选：D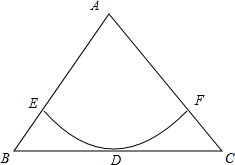
点评 本题考查几何概型，涉及正三角形的面积和扇形的面积，属中档题．
练习册系列答案
相关题目
10．已知命题p：在△ABC中，若A＞B，则$\frac{co{s}^{2}B}{co{s}^{2}A}$＞1；命题q：?x∈（0，+∞），$\frac{1}{{x}^{2}}$+$\frac{1}{x}$≥2，在命题（1）p∧q；（2）p∨q；（3）（￢p）∨q；（4）p∧（￢q）中，真命题是（ ）
| A． | （1）（3） | B． | （2）（4） | C． | （1）（4） | D． | （2）（3） |
8．一个几何体的三视图如图所示，则这个几何体的体积为（ ）
| A． | $\frac{（9+2π）\sqrt{3}}{6}$ | B． | $\frac{（8+2π）\sqrt{3}}{6}$ | C． | $\frac{（6+π）\sqrt{3}}{6}$ | D． | $\frac{（8+π）\sqrt{3}}{6}$ |
15．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=3，且$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影与$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影相等，则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{10}$ | C． | 2$\sqrt{2}$ | D． | 2 |
5．“m＞0”是“函数f（x）=m+log2x（x≥1）不存在零点”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
12．把A、B、C、D四件玩具分给三个小朋友，每位小朋友至少分到一件玩具，且A、B两件玩具不能分给同一个人，则不同的分法有（ ）
| A． | 36种 | B． | 30种 | C． | 24种 | D． | 18种 |
如图，在平面直角坐标系x Oy中，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，左顶点 A与上顶点 B的距离为$\sqrt{6}$．