题目内容
观察下列一组等式:
①sin2300+cos2600+sin300cos600=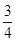 ,②sin2150+cos2450+sin150cos450=
,②sin2150+cos2450+sin150cos450=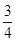 ,
,
③sin2450+cos2750+sin450cos750=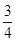 ,……,
,……,
那么,类比推广上述结果,可以得到的一般结果是: _____.
①sin2300+cos2600+sin300cos600=
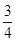 ,②sin2150+cos2450+sin150cos450=
,②sin2150+cos2450+sin150cos450=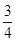 ,
,③sin2450+cos2750+sin450cos750=
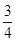 ,……,
,……,那么,类比推广上述结果,可以得到的一般结果是: _____.
sin2 + cos2 (30°+x)=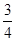 ,本题答案不唯一,与之等价的均可。
,本题答案不唯一,与之等价的均可。
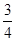 ,本题答案不唯一,与之等价的均可。
,本题答案不唯一,与之等价的均可。解:因为观察下列一组等式:
①sin2300+cos2600+sin300cos600=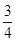 ,②sin2150+cos2450+sin150cos450=
,②sin2150+cos2450+sin150cos450=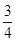 ,
,
③sin2450+cos2750+sin450cos750=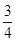 ,……,
,……,
那么,类比推广上述结果,可以得到的一般结果是:sin2 + cos2 (30°+x)=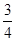 ,
,
①sin2300+cos2600+sin300cos600=
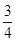 ,②sin2150+cos2450+sin150cos450=
,②sin2150+cos2450+sin150cos450=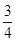 ,
,③sin2450+cos2750+sin450cos750=
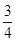 ,……,
,……,那么,类比推广上述结果,可以得到的一般结果是:sin2 + cos2 (30°+x)=
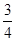 ,
,
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
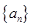 满足:
满足: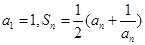 ,其中
,其中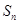 为其前
为其前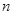 项和,则
项和,则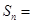 ____________
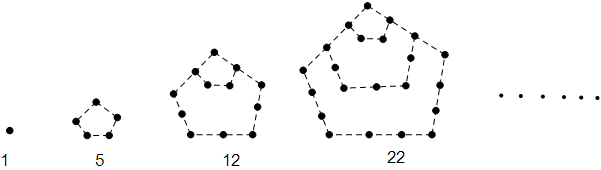
____________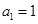 ,第2个五角形数记作
,第2个五角形数记作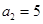 ,第3个五角形数记作
,第3个五角形数记作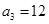 ,第4个五角形数记作
,第4个五角形数记作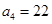 ,……,若按此规律继续下去,若
,……,若按此规律继续下去,若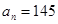 ,则
,则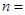 .
.
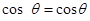 ;
;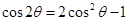 ;
;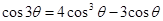 ;
;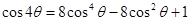 ;
;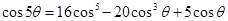 .
.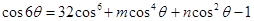 ,其中
,其中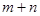 =_______.
=_______.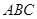 中,
中,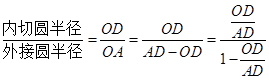 ,
,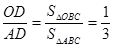 ,所以
,所以 。应用类比推理,在正四面体
。应用类比推理,在正四面体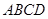 (每个面都是正三角形的四面体)中,
(每个面都是正三角形的四面体)中,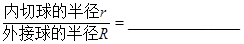 。
。 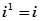 ,
,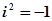 ,
, ,
,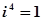 ,
,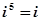 ,由此可猜想
,由此可猜想 ____________
____________