题目内容
在△ABC中,角 所对的边分别为
所对的边分别为 ,
, 且
且 ∥
∥
(Ⅰ)求 的值
的值
(Ⅱ)求三角函数式 的取值范围
的取值范围
(Ⅰ)  ;(Ⅱ)三角函数式
;(Ⅱ)三角函数式 的取值范围为(-1,
的取值范围为(-1, ].
].
解析试题分析:(I)求 的值,可考虑利用正弦定理,也可利用面积公式
的值,可考虑利用正弦定理,也可利用面积公式 ,但本题由已知
,但本题由已知 且
且 ∥
∥ ,可根据向量平行的充要条件列式:
,可根据向量平行的充要条件列式: ,结合正弦定理与正弦的诱导公式,两角和的正弦公式化简整理,化简可得
,结合正弦定理与正弦的诱导公式,两角和的正弦公式化简整理,化简可得 ,可得
,可得 ,从而得到
,从而得到 的值;(II)求三角函数式
的值;(II)求三角函数式 的取值范围,将三角函数式用二倍角的余弦公式结合“切化弦”,化简整理得
的取值范围,将三角函数式用二倍角的余弦公式结合“切化弦”,化简整理得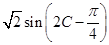 ,再根据
,再根据 算出
算出 的范围,得到
的范围,得到 的取值范围,最终得到原三角函数式的取值范围.
的取值范围,最终得到原三角函数式的取值范围.
试题解析:(Ⅰ)∵ 且
且 ∥
∥ ,∴
,∴
由正弦定理得2sinAcosC=2sinB-sinC, 又sinB=sin(A+C)=sinAcosC+cosAsinC,∴ sinC=cosAsinC
sinC=cosAsinC
∵sinC≠0 ∴cosA= ,
,
又∵0<A<p, ∴A= , ∴
, ∴
(Ⅱ)原式= +1=1-
+1=1- =1-2cos2C+2sinCcosC=sin2C-cos2C=
=1-2cos2C+2sinCcosC=sin2C-cos2C=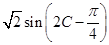
∵0<C< p ∴
p ∴ <2C-
<2C- <
< , ∴
, ∴ < sin(2C-
< sin(2C- )≤1
)≤1
∴-1< sin(2C-
sin(2C- )≤
)≤ , 即三角函数式
, 即三角函数式 的取值范围为(-1,
的取值范围为(-1, ]
]
考点:三角函数中的恒等变换应用;平面向量共线(平行)的坐标表示.

练习册系列答案
相关题目
 sin ωx-sin2
sin ωx-sin2 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π. 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围. ,
, ,函数
,函数 。
。 的值域和函数的单调递增区间;
的值域和函数的单调递增区间;  ,且
,且 时,求
时,求 的值.
的值. .
. 在角
在角 的终边上,求
的终边上,求 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求
,求 的值域.
的值域. ;
; 为第二象限角,化简
为第二象限角,化简 .
. 中,已知
中,已知 .
. ;
;  求角A的大小.
求角A的大小. ,
, ,且
,且 。
。 )取最大值时,判断三角形ABC的形状。
)取最大值时,判断三角形ABC的形状。 (
( )的最小正周期为
)的最小正周期为 .求函数
.求函数 的单调增区间;
的单调增区间; 中,角
中,角 对边分别是
对边分别是 ,且满足
,且满足 .若
.若 ,
, .求角
.求角 的大小和边b的长.
的大小和边b的长.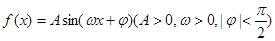 的图象的一部分如下图所示.
的图象的一部分如下图所示.
 的解析式;
的解析式; 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.