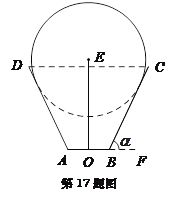
题目内容
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左顶点、右焦点,点
的左顶点、右焦点,点![]() 为椭圆
为椭圆![]() 上一动点,当
上一动点,当![]() 轴时,
轴时, ![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若椭圆![]() 存在点
存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形(点
是平行四边形(点![]() 在第一象限),求直线
在第一象限),求直线![]() 与
与![]() 的斜率之积;
的斜率之积;
(3)记圆![]() 为椭圆
为椭圆![]() 的“关联圆”. 若
的“关联圆”. 若![]() ,过点
,过点![]() 作椭圆
作椭圆![]() 的“关联圆”的两条切线,切点为
的“关联圆”的两条切线,切点为![]() 、
、![]() ,直线
,直线![]() 的横、纵截距分别为
的横、纵截距分别为![]() 、
、![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:
(1)利用题意得到关于![]() 的齐次方程,求解方程组可得椭圆的离心率
的齐次方程,求解方程组可得椭圆的离心率![]() ;
;
(2) 由题意, ![]() ,
, ![]() ,则
,则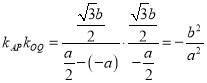 ,结合(1)的结论可得
,结合(1)的结论可得![]() .
.
(3) 由(1)知椭圆![]() 方程为
方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
四边形![]() 的外接圆方程为
的外接圆方程为![]() ,
,
所以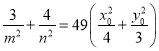 ,因为点
,因为点![]() 在椭圆
在椭圆![]() 上,则
上,则![]() .
.
试题解析:
解:(1)由![]() 轴,知
轴,知![]() ,代入椭圆
,代入椭圆![]() 的方程,
的方程,
得![]() ,解得
,解得![]() .
.
又![]() ,所以
,所以![]() ,解得
,解得![]() .
.
(2)因为四边形![]() 是平行四边形,所以
是平行四边形,所以![]() 且
且![]() 轴,
轴,
所以![]() ,代入椭圆
,代入椭圆![]() 的方程,解得
的方程,解得![]() , 因为点
, 因为点![]() 在第一象限,所以
在第一象限,所以![]() ,同理可得
,同理可得![]() ,
, ![]() , 所以
, 所以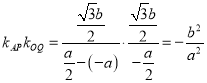 ,
,
由(1)知![]() ,得
,得![]() ,所以
,所以![]() .
.
(3)由(1)知![]() ,又
,又![]() ,解得
,解得![]() ,所以椭圆
,所以椭圆![]() 方程为
方程为![]() ,
,
圆![]() 的方程为
的方程为![]() ①. 连接
①. 连接![]() ,由题意可知,
,由题意可知, ![]() ,
, ![]() ,
,
所以四边形![]() 的外接圆是以
的外接圆是以![]() 为直径的圆,
为直径的圆,
设![]() ,则四边形
,则四边形![]() 的外接圆方程为
的外接圆方程为![]() ,
,
即![]() ②. ①-②,得直线
②. ①-②,得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() . 所以
. 所以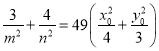 ,
,
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,所以
,所以![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目