题目内容
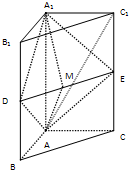 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=1,AA1=2,D、E分别是BB1、CC1的中点,M是DE的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=1,AA1=2,D、E分别是BB1、CC1的中点,M是DE的中点.(1)求证:平面ADE⊥平面AMA1;
(2)试问能否在线段AC1上找一点N,使得直线MN与平面ADA1平行?请说明理由;
(3)求三棱锥A1-ADE的体积.
分析:(1)证明平面ADE⊥平面AMA1,需证明其中一个平面经过另一个平面的一条垂线,由M为DE的中点,可由已知条件得到AD=AE,A1D=A1E,由线面垂直的判定得到DE⊥平面A1AM,从而由面面垂直的判定得到结论;
(2)由M为DE的中点,可猜测取N为AC1中点,连结BC1后由三角形的中位线的性质得到直线MN与平面ADA1平行;
(3)借助于等积法把三棱锥A1-ADE的体积转化为三棱锥D-A1AE的体积求解.
(2)由M为DE的中点,可猜测取N为AC1中点,连结BC1后由三角形的中位线的性质得到直线MN与平面ADA1平行;
(3)借助于等积法把三棱锥A1-ADE的体积转化为三棱锥D-A1AE的体积求解.
解答: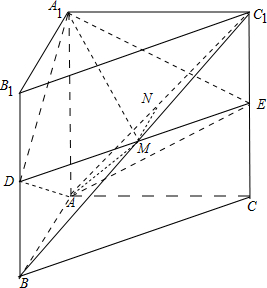 (1)证明:如图,
(1)证明:如图,
在直三棱柱ABC-A1B1C1中,∵AB=AC=1,且D、E分别是BB1、CC1的中点,
∴可得AD=AE,A1D=A1E,又M是DE的中点,
∴AM⊥DE,A1M⊥DE,又AM∩A1M=M,
∴DE⊥平面A1AM,而DE?平面ADE,∴平面ADE⊥平面AMA1;
(2)解:N为AC1中点时,直线MN与平面ADA1平行.
事实上,连结BC1,则M∈BC1,
M是BC1的中点,N为AC1的中点,
∴MN∥AB,又AB?ADA1,MN?ADA1,
∴直线MN与平面ADA1平行;
(3)∵在直三棱柱ABC-A1B1C1中,AB⊥AC,∴AB⊥平面A1AE.
即AB的长度为D到平面A1AE的距离,而S△A1AE=
AC•AA1=
×1×2=1.
∴VA1-ADE=VD-A1AE=
S△A1AE•AB=
×1×1=
.
 (1)证明:如图,
(1)证明:如图,在直三棱柱ABC-A1B1C1中,∵AB=AC=1,且D、E分别是BB1、CC1的中点,
∴可得AD=AE,A1D=A1E,又M是DE的中点,
∴AM⊥DE,A1M⊥DE,又AM∩A1M=M,
∴DE⊥平面A1AM,而DE?平面ADE,∴平面ADE⊥平面AMA1;
(2)解:N为AC1中点时,直线MN与平面ADA1平行.
事实上,连结BC1,则M∈BC1,
M是BC1的中点,N为AC1的中点,
∴MN∥AB,又AB?ADA1,MN?ADA1,
∴直线MN与平面ADA1平行;
(3)∵在直三棱柱ABC-A1B1C1中,AB⊥AC,∴AB⊥平面A1AE.
即AB的长度为D到平面A1AE的距离,而S△A1AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴VA1-ADE=VD-A1AE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查了直线与平面平行的判定,考查了平面与平面垂直的判定,训练了利用等积法求棱锥的体积,考查了学生的空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目




