题目内容
已知二次函数f(x)=ax2+8x+3.
(1)若函数f(x)=ax2+8x+3的图象恒在直线y=5的下方,求实数a的范围;
(2)对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立.问a为何值时l(a)最大?求出这个最大的l(a),证明你的结论.
(1)若函数f(x)=ax2+8x+3的图象恒在直线y=5的下方,求实数a的范围;
(2)对于给定的负数a,有一个最大的正数l(a),使得在整个区间[0,l(a)]上,不等式|f(x)|≤5都成立.问a为何值时l(a)最大?求出这个最大的l(a),证明你的结论.
分析:(1)函数f(x)=ax2+8x+3的图象恒在直线y=5的下方,等价于f(x)max<5,配方后可求f(x)的最大值;
(2)当3-
>5,3-
≤5两种情况进行讨论:作出图象,借助图象可转化为解方程|f(x)|=5,根据根的情况可求;
(2)当3-
| 16 |
| a |
| 16 |
| a |
解答: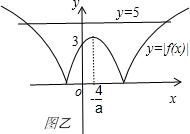
 解:(1)将f(x)配方得:f(x)=a(x+
解:(1)将f(x)配方得:f(x)=a(x+
)2+3-
,
由于a<0,于是f(x)max=3-
.
因为函数f(x)=ax2+8x+3的图象恒在直线y=5的下方,所以3-
<5,解得a<-8;
(2)分①当3-
>5,即-8<a<0时,如左图所示:
有l(a)∈(0,-
),且f(l(a))=5.
令ax2+8x+3=5,于是方程有两不等实数根.
由于函数y=f(x)=ax2+8x+3的图象关于直线x=-
对称,
故方程的一根大于-
,另一根小于-
,l(a)只能取方程ax2+8x+3=5的较小根,
于是l(a)=
=
<
=
.
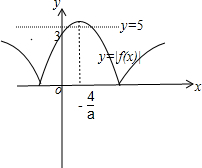
②当3-
≤5,即a≤-8时,如右图(乙),
有l(a)>-
,且f(l(a))=-5.
令ax2+8x+3=-5,于是方程有两不等实数根.
且方程的一根大于-
,另一根小于-
,l(a)必须取方程ax2+8x+3=-5的较大根,
于是l(a)=
=
≤
=
,当且仅当a=-8时,取“=”.
因
>
,
故可取l(a)=
为最大,此时a=-8.

 解:(1)将f(x)配方得:f(x)=a(x+
解:(1)将f(x)配方得:f(x)=a(x+| 4 |
| a |
| 16 |
| a |
由于a<0,于是f(x)max=3-
| 16 |
| a |
因为函数f(x)=ax2+8x+3的图象恒在直线y=5的下方,所以3-
| 16 |
| a |
(2)分①当3-
| 16 |
| a |
有l(a)∈(0,-
| 4 |
| a |
令ax2+8x+3=5,于是方程有两不等实数根.
由于函数y=f(x)=ax2+8x+3的图象关于直线x=-
| 4 |
| a |
故方程的一根大于-
| 4 |
| a |
| 4 |
| a |
于是l(a)=
-4+
| ||
| a |
| 2 | ||
|
| 2 |
| 4 |
| 1 |
| 2 |
②当3-
| 16 |
| a |
有l(a)>-
| 4 |
| a |
令ax2+8x+3=-5,于是方程有两不等实数根.
且方程的一根大于-
| 4 |
| a |
| 4 |
| a |
于是l(a)=
-4-
| ||
| a |
| 4 | ||
|
| 4 | ||
|
| ||
| 2 |
因
| ||
| 2 |
| 1 |
| 2 |
故可取l(a)=
| ||
| 2 |
点评:(1)对于二次函数与二次方程及二次不等式相结合的问题,常常画出示意图,利用图形的直观性进行问题的等价变形,直至问题的最终解决;(2)容易误认为第(1)种情形下方程的最小根为
,第(2)种情形下方程的最大根为
.
-4-
| ||
| a |
-4+
| ||
| a |

练习册系列答案
相关题目