题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() ,
,![]() 为两个不相等的正数,证明:
为两个不相等的正数,证明:![]() .
.
【答案】(1)![]() 时,
时,![]() 在区间
在区间![]() 内为增函数;
内为增函数;![]() 时,
时,![]() 在区间
在区间![]() 内为增函数;
内为增函数;![]() 在区间
在区间![]() 内为减函数; (2)见解析.
内为减函数; (2)见解析.
【解析】
(1)求出![]() ,分两种种情况讨论
,分两种种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)设
的减区间;(2)设![]() ,原不等式等价于
,原不等式等价于 ,令
,令![]() ,则原不等式也等价于即
,则原不等式也等价于即![]() .设
.设![]() ,利用导数可得
,利用导数可得![]() 在区间
在区间![]() 内为增函数,
内为增函数,![]() ,从而可得结论.
,从而可得结论.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
若![]() ,
,![]() ,则
,则![]() 在区间
在区间![]() 内为增函数;
内为增函数;
若![]() ,令
,令![]() ,得
,得![]() .则当
.则当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 内为增函数;当
内为增函数;当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 内为减函数.
内为减函数.
(2)当![]() 时,
时,![]() .不妨设
.不妨设![]() ,则原不等式等价于
,则原不等式等价于 ,
,
令![]() ,则原不等式也等价于即
,则原不等式也等价于即![]() .
.
下面证明当![]() 时,
时,![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,
,
故![]() 在区间
在区间![]() 内为增函数,
内为增函数,![]() ,即
,即![]() ,
,
所以![]() .
.

练习册系列答案
相关题目
【题目】为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处.现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示.
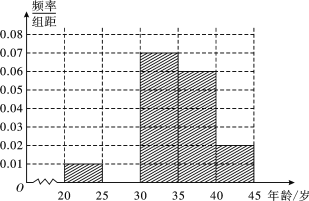
分组(单位:岁) | 频数 | 频率 |
| 5 |
|
| ① |
|
|
| ② |
|
|
|
|
|
|
合计 |
|
|
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.