题目内容
19.已知函数f(x)=2x3+3ax2+3bx+8在x=1及x=2处取得极值.(1)求a、b的值;
(2)求f(x)的单调区间.
分析 (1)求出函数的导数,利用函数的极值点,列出方程组,求解a,b即可.
(2)利用函数的极值点,结合导函数的符号,推出函数的单调区间即可.
解答 解:(1)由已知函数f(x)=2x3+3ax2+3bx+8,
可得f′(x)=6x2+6ax+3b
因为f(x)在x=1及x=2处取得极值,所以1和2是方程f′(x)=6x2+6ax+3b=0的两根,
故$\left\{\begin{array}{l}6+6a+3b=0\\ 24+12a+3b=0\end{array}\right.$
解得:a=-3、b=4.
(2)由(1)可得f(x)=2x3-9x2+12x+8,
可得 f′(x)=6x2-18x+12=6(x-1)(x-2)
当x<1或x>2时,f′(x)>0,f(x)是增加的;
当1<x<2时,f′(x)<0,f(x)是减少的.
所以,f(x)的单调增区间为(-∞,1)和(2,+∞),f(x)的单调减区间为(1,2).
点评 本题考查导函数的应用,函数的极值以及函数的单调区间的求法,考查计算能力.

练习册系列答案
相关题目
10.若f(x)=$\root{3}{2x+4}$,则f(2)=( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
9.已知y=f(x)是定义在R上的偶函数,其对任意的x1,x2∈(-∞,0],都使(x2-x1)[f(x2)-f(x1)]<0成立,则当f(sinx)>f(cosx)时,x的取值范围( )
| A. | (2kπ-$\frac{π}{4}$,2kπ+$\frac{π}{4}$),k∈Z | B. | (kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$),k∈Z | ||
| C. | (2kπ+$\frac{π}{4}$,2kπ+$\frac{3π}{4}$),k∈Z | D. | (kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$),k∈Z |
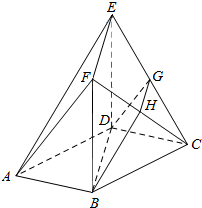 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.