题目内容
7.已知函数f(x)=x2+2ax+1-a在区间[0,1]上的最大值是2,求实数a的值.分析 先求出函数的对称轴,通过讨论a的范围,得到函数的单调区间,求出函数的最大值的表达式,解出即可.
解答 解:函数f(x)=x2+2ax+1-a,
对称轴是x=-a,
当-a≤0即a≥0时:f(x)在[0,1]递增,
∴f(x)max=f(1)=a+2=2,解得:a=0;
当0<-a<$\frac{1}{2}$即-$\frac{1}{2}$<a<0时:f(x)在[0,a)递减,在(a,1],
∴f(x)max=f(1)=a+2=2,解得:a=0;
当$\frac{1}{2}$≤-a<1即-1<a≤-$\frac{1}{2}$时:f(x)在[0,a)递减,在(a,1],
∴f(x)max=f(0)=1-a=2,解得:a=-1;
当-a≥1即a≤-1时:f(x)在[0,1]递减,
∴f(x)max=f(0)=1-a=2,解得:a=-1.
点评 本题考查了二次函数的性质,考查分类讨论思想,是一道基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
15.下列函数在(0,+∞)上是减函数的是( )
| A. | y=x2 | B. | y=-x2 | C. | y=-2x2+3x-1 | D. | y=x |
2.欧阳修《煤炭翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿.
可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为1.5cm圆,中间有边长为0.5cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为( )
可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为1.5cm圆,中间有边长为0.5cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为( )
| A. | $\frac{4}{9π}$ | B. | $\frac{9}{4π}$ | C. | $\frac{4π}{9}$ | D. | $\frac{9π}{4}$ |
12.若全集U={0,1,2,3}且∁UA={2},则集合A为( )
| A. | A={0,1} | B. | A={0,1,3} | C. | A={0,1,2,3} | D. | A={1,3} |
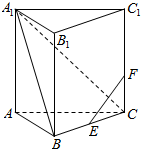 如图,已知直三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,点F在侧棱CC1上,且CF=1,求证:EF⊥A1C.
如图,已知直三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,点F在侧棱CC1上,且CF=1,求证:EF⊥A1C.