题目内容
4.已知f(x)是定义在R上的奇函数,当x≥0时f(x)=3x+m(m为常数),则m=-1,f(-log35)的值为-4.分析 由题设条件可先由函数在R上是奇函数求出参数m的值,求函数函数的解板式,将x=-log35代入解析式即可求得所求的函数值.
解答 解:由题意,f(x)是定义在R上的奇函数,
当x≥0时f(x)=3x+m(m为常数),
∴f(0)=30+m=0,解得m=-1,
故有x≥0时f(x)=3x-1,
∴f(-log35)=-f(log35)=-(${3}^{lo{g}_{3}5}$-1)=-(5-1)=-4,
故答案为:-1,-4.
点评 本题考查函数奇偶性质,解题的关键是利用f(0)=0求出参数m的值,再利用性质转化求值,本题考查了转化的思想,方程的思想.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
15.下列函数在(0,+∞)上是减函数的是( )
| A. | y=x2 | B. | y=-x2 | C. | y=-2x2+3x-1 | D. | y=x |
12.若全集U={0,1,2,3}且∁UA={2},则集合A为( )
| A. | A={0,1} | B. | A={0,1,3} | C. | A={0,1,2,3} | D. | A={1,3} |
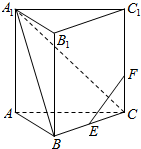 如图,已知直三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,点F在侧棱CC1上,且CF=1,求证:EF⊥A1C.
如图,已知直三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,点F在侧棱CC1上,且CF=1,求证:EF⊥A1C.