题目内容
已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为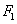 和
和 ,且|
,且|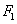
 |=2,
|=2,
点(1, )在该椭圆上.
)在该椭圆上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过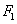 的直线
的直线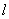 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A B的面积为
B的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线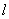 相切是圆的方程.
相切是圆的方程.
【答案】
(1)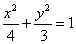 (2)
(2)
【解析】
试题分析:解:(Ⅰ)椭圆C的方程为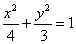
(Ⅱ)①当直线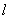 ⊥x轴时,可得A(-1,-
⊥x轴时,可得A(-1,-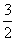 ),B(-1,
),B(-1,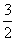 ),
), A
A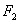 B的面积为3,不符合题意.
B的面积为3,不符合题意.
②当直线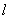 与x轴不垂直时,设直线
与x轴不垂直时,设直线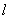 的方程为y=k(x+1).代入椭圆方程得:
的方程为y=k(x+1).代入椭圆方程得:
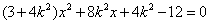 ,显然
,显然 >0成立,设A
>0成立,设A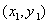 ,B
,B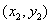 ,则
,则
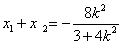 ,
,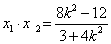 ,可得|AB|=
,可得|AB|=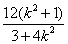
又圆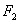 的半径r=
的半径r=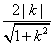 ,∴
,∴ A
A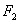 B的面积=
B的面积=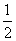 |AB| r=
|AB| r=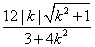 =
=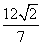 ,化简得:17
,化简得:17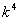 +
+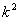 -18=0,得k=±1,∴r =
-18=0,得k=±1,∴r =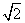 ,圆的方程为
,圆的方程为
考点:直线与椭圆的位置关系的运用
点评:主要是考查了直线与椭圆的位置关系的运用,通过联立方程组,结合韦达定理来求解三角形的面积,属于基础题。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
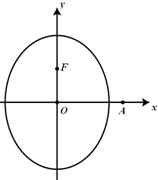 (2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=
(2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=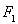
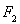
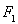
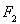
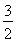
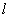

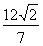
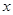 轴上,离心率为
轴上,离心率为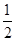 ,且点
,且点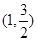 在该椭圆上。
在该椭圆上。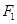 的直线
的直线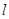 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若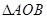 的面积为
的面积为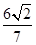 ,求圆心在原点O且与直线相切的圆的方程。
,求圆心在原点O且与直线相切的圆的方程。