题目内容
已知椭圆C的对称中心为原点O,焦点在x轴上,左右焦点分别为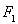 和
和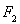 ,且|
,且|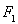
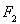 |=2,
|=2,
点(1,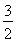 )在该椭圆上.
)在该椭圆上.
(1)求椭圆C的方程;
(2)过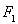 的直线
的直线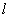 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A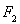 B的面积为
B的面积为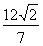 ,求以
,求以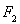 为圆心且与直线
为圆心且与直线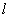 相切圆的方程.
相切圆的方程.
【答案】
(1)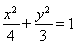 ;(2)
;(2)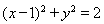 .
.
【解析】
试题分析:本题主要考查椭圆的定义和方程、圆的方程、点到直线的距离公式等基础知识,同时考查解析几何的基本思想方法和运算求解能力.第一问,利用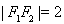 ,得
,得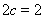 ,即
,即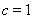 ,再根据点在椭圆上,得到
,再根据点在椭圆上,得到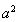 和
和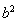 的值,从而得到椭圆方程;第二问,分2种情况进行讨论,当直线
的值,从而得到椭圆方程;第二问,分2种情况进行讨论,当直线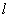 垂直x轴时,
垂直x轴时,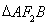 的面积很容易求出,与已知面积不相等,所以舍掉,当直线
的面积很容易求出,与已知面积不相等,所以舍掉,当直线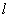 不垂直x轴时,设出直线方程与椭圆方程联立,利用韦达定理,求出
不垂直x轴时,设出直线方程与椭圆方程联立,利用韦达定理,求出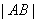 ,再数形结合求出圆
,再数形结合求出圆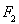 的半径,从而求
的半径,从而求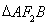 的面积,解出k的值,确定半径的值,即可求出圆的方程.
的面积,解出k的值,确定半径的值,即可求出圆的方程.
试题解析:(1)椭圆C的方程为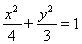 ..(4分)
..(4分)
(2)①当直线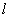 ⊥x轴时,可得
⊥x轴时,可得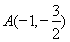 ,
,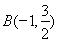 ,
, 的面积为3,不符合题意. (6分)
的面积为3,不符合题意. (6分)
②当直线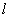 与x轴不垂直时,设直线
与x轴不垂直时,设直线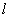 的方程为y=k(x+1).代入椭圆方程得:
的方程为y=k(x+1).代入椭圆方程得:
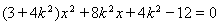 ,显然
,显然 >0成立,设A
>0成立,设A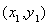 ,B
,B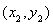 ,则
,则
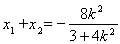 ,
,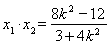 ,可得|AB|=
,可得|AB|=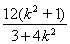 ..(9分)
..(9分)
又圆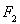 的半径
的半径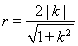 ,∴
,∴ 的面积
的面积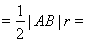
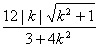 =
=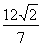 ,化简得:
,化简得: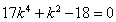 ,得k=±1,∴r =
,得k=±1,∴r =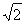 ,圆的方程为
,圆的方程为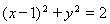 ..(12分)
..(12分)
考点:1.椭圆的定义和方程;2.圆的方程;3.点到直线的距离公.

练习册系列答案
相关题目
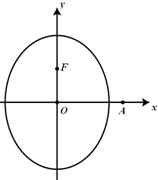 (2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=
(2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=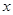 轴上,离心率为
轴上,离心率为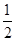 ,且点
,且点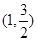 在该椭圆上。
在该椭圆上。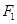 的直线
的直线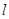 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若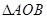 的面积为
的面积为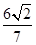 ,求圆心在原点O且与直线相切的圆的方程。
,求圆心在原点O且与直线相切的圆的方程。