题目内容
已知椭圆C的对称中心为原点O,焦点在x轴上,离心率为| 1 |
| 2 |
| 3 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C的左焦点F1的直线l与椭圆C相交于A,B两点,若△AOB的面积为
6
| ||
| 7 |
分析:(Ⅰ)设出椭圆的标准方程,根据离心率求得a和c关系,进而根据a2=b2+c2,求得a和b的关系,把点C坐标代入椭圆方程求得a,进而求得b,则椭圆方程可得.
(Ⅱ)先看当l与x轴垂直时,可求得A,B的坐标,进而求得三角形AOB的坐标,不符合题意;再看直线l斜率存在时,设出直线方程,与椭圆方程联立消去y,设A(x1,y1),B(x2,y2),进而求得x1+x2和x1x2的表达式,进而表示出|AB|,进而求得圆的半径后表示出三角形AOB的面积,求得k,进而求得圆的半径,则圆的方程可得.
(Ⅱ)先看当l与x轴垂直时,可求得A,B的坐标,进而求得三角形AOB的坐标,不符合题意;再看直线l斜率存在时,设出直线方程,与椭圆方程联立消去y,设A(x1,y1),B(x2,y2),进而求得x1+x2和x1x2的表达式,进而表示出|AB|,进而求得圆的半径后表示出三角形AOB的面积,求得k,进而求得圆的半径,则圆的方程可得.
解答:解:(Ⅰ)设椭圆C的方程为
+
=1,(a>b>0),由题意可得e=
=
,
又a2=b2+c2,所以b2=
a2
因为椭圆C经过(1,
),代入椭圆方程有
+
=1
解得a=2
所以c=1,b2=4-1=3故椭圆C的方程为
+
=1.
(Ⅱ)当直线l⊥x轴时,计算得到:A(-1,-
),B(-1,
),
S△AOB=
•|AB|•|OF1|=
×1×3=
,不符合题意.
当直线l与x轴不垂直时,设直线l的方程为:y=k(x+1),k≠0
由
,消去y,得(3+4k2)x2+8k2x+4k2-12=0
显然△>0成立,设A(x1,y1),B(x2,y2),
则x1+x2=-
,x1•x2=
又|AB|=
=
=
•
=
•
=
即|AB|=
•
=
又圆O的半径r=
=
所以S△AOB=
•|AB|•r=
•
•
=
=
化简,得17k4+k2-18=0,即(k2-1)(17k2+18)=0,
解得k12=1,k22=-
(舍)
所以,r=
=
,故圆O的方程为:x2+y2=
.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| 1 |
| 2 |
又a2=b2+c2,所以b2=
| 3 |
| 4 |
因为椭圆C经过(1,
| 3 |
| 2 |
| 1 |
| a2 |
| ||
|
解得a=2
所以c=1,b2=4-1=3故椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)当直线l⊥x轴时,计算得到:A(-1,-
| 3 |
| 2 |
| 3 |
| 2 |
S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
当直线l与x轴不垂直时,设直线l的方程为:y=k(x+1),k≠0
由
|
显然△>0成立,设A(x1,y1),B(x2,y2),
则x1+x2=-
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
又|AB|=
| (x1-x2)2+(y1-y2)2 |
| (x1-x2)2+k2(x1-x2)2 |
=
| 1+k2 |
| (x1-x2)2 |
| 1+k2 |
| (x1+x2)2-4x1•x2 |
=
| 1+k2 |
|
即|AB|=
| 1+k2 |
12
| ||
| 3+4k2 |
| 12(k2+1) |
| 3+4k2 |
又圆O的半径r=
| |k×0-0+k| | ||
|
| |k| | ||
|
所以S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 12(k2+1) |
| 3+4k2 |
| |k| | ||
|
6|k|
| ||
| 3+4k2 |
6
| ||
| 7 |
化简,得17k4+k2-18=0,即(k2-1)(17k2+18)=0,
解得k12=1,k22=-
| 18 |
| 17 |
所以,r=
| |k| | ||
|
| ||
| 2 |
| 1 |
| 2 |
点评:本题主要考查了椭圆的标准方程,涉及了椭圆与直线,圆的关系,综合性强.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
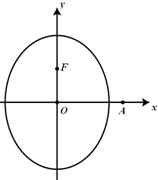 (2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=
(2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=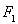
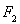
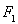
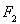
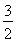
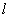

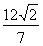
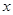 轴上,离心率为
轴上,离心率为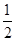 ,且点
,且点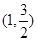 在该椭圆上。
在该椭圆上。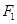 的直线
的直线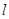 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若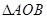 的面积为
的面积为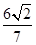 ,求圆心在原点O且与直线相切的圆的方程。
,求圆心在原点O且与直线相切的圆的方程。