题目内容
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,AB=2,且PB⊥底面ABCD.
(Ⅰ)试在棱PB上求一点M,使CM∥平面PDA;
(Ⅱ)在(Ⅰ)的结论下,求三棱锥P-ADM的体积.
分析:(Ⅰ)取PB得中点M,则有CM∥平面PDA,证明如下:取AB中点N,则MN∥PA,PA?平面PDA,MN?平面PDA,所以MN∥平面PDA.由题意得四边形ANCD是平行四边形,所以CN∥AD,AD?平面PDA,CN?平面PDA,所以CN∥平面PDA,所以平面MCN∥平面PDA,∴CN∥平面PDA.
(Ⅱ)由(Ⅰ):M为PB的中点,则VP-ADM=VB-ADM,在△ABD中,AB-2,AB边上的高h=BC=1,∴s△ABD=
•AB•h=1
BM=
,所以三棱锥P-ADM的体积是
.
(Ⅱ)由(Ⅰ):M为PB的中点,则VP-ADM=VB-ADM,在△ABD中,AB-2,AB边上的高h=BC=1,∴s△ABD=
| 1 |
| 2 |
BM=
| 1 |
| 2 |
| 1 |
| 6 |
解答:解:(Ⅰ)取PB得中点M,则有CM∥平面PDA,证明如下:
取AB中点N,则MN∥PA,PA?平面PDA,MN?平面PDA,
∴MN∥平面PDA
连接CN,则AN∥CD且AN=CD=1,
∴四边形ANCD是平行四边形
∴CN∥AD,AD?平面PDA,CN?平面PDA,
∴CN∥平面PDA
又MN∩CN=N,∴平面MCN∥平面PDA,CM?平面MCN
∴CN∥平面PDA.
(Ⅱ)由(Ⅰ):M为PB的中点,则VP-ADM=VB-ADM
在△ABD中,AB-2,AB边上的高h=BC=1,
∴s△ABD=
•AB•h=1
BM=
,∴VM-ABD =
•BM•S△ABD=
所以三棱锥P-ADM的体积是
.
取AB中点N,则MN∥PA,PA?平面PDA,MN?平面PDA,
∴MN∥平面PDA
连接CN,则AN∥CD且AN=CD=1,
∴四边形ANCD是平行四边形
∴CN∥AD,AD?平面PDA,CN?平面PDA,
∴CN∥平面PDA
又MN∩CN=N,∴平面MCN∥平面PDA,CM?平面MCN
∴CN∥平面PDA.
(Ⅱ)由(Ⅰ):M为PB的中点,则VP-ADM=VB-ADM
在△ABD中,AB-2,AB边上的高h=BC=1,
∴s△ABD=
| 1 |
| 2 |
BM=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
所以三棱锥P-ADM的体积是
| 1 |
| 6 |
点评:解决探索性问题应该先利用代点检验的方法找到点,一般是线段的端点或线段的中点,求三棱锥的体积时当三棱锥的高与底面积不易求时,应该根据条件判断是否存在于已知三棱锥体积相等的三棱锥.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,已知正方体ABCD-A1B1C1D1,则下列四个命题:
如图,已知正方体ABCD-A1B1C1D1,则下列四个命题: (2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.
(2008•湖北模拟)如图,已知四棱锥S-ABCD中,△SAD是边长为a的正三角形,平面SAD⊥平面ABCD,四边形ABCD为菱形,∠DAB=60°,P为AD的中点,Q为SB的中点.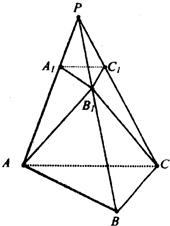 (2008•河西区三模)如图,已知三棱锥P-ABC,A1,B1,C1分别在棱PA、PB、PC上,且面A1B1C1∥面ABC,又面AB1C⊥面ABC.△AB1C为边长是4的等边三角形,∠ACB=90°,BC=2.
(2008•河西区三模)如图,已知三棱锥P-ABC,A1,B1,C1分别在棱PA、PB、PC上,且面A1B1C1∥面ABC,又面AB1C⊥面ABC.△AB1C为边长是4的等边三角形,∠ACB=90°,BC=2.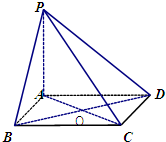 (2012•上海二模)如图,在四棱锥P-ABCD中,已知AC与BD交于点O,PA⊥平面ABCD,底面ABCD是边长为4的菱形,∠BAD=12°,PA=4.
(2012•上海二模)如图,在四棱锥P-ABCD中,已知AC与BD交于点O,PA⊥平面ABCD,底面ABCD是边长为4的菱形,∠BAD=12°,PA=4.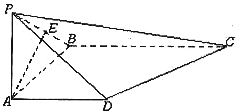 如图,在四棱锥P-ABCD中,PA,AB,AD两两互相垂直,已知AD∥BC,BC=2AD,E是PB的中点.
如图,在四棱锥P-ABCD中,PA,AB,AD两两互相垂直,已知AD∥BC,BC=2AD,E是PB的中点.