题目内容
如图,一辆汽车从O点出发,沿海岸一条直线公路以100千米/时的速度向东匀速行驶,汽车开动时,在O点南偏东方向距O点500千米且与海岸距离MQ为300千米的海上M处有一快艇,与汽车同时出发,要把一件重要的物品递送给这辆汽车的司机,问快艇至少须以多大的速度行驶,才能把物品递送到司机手中,并求快艇以最小速度行驶时的方向与OM所成的角.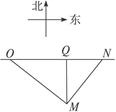

解:设快艇从M处以v千米/时的速度出发,沿MN方向航行,
t小时 后与汽车相遇………………………………1分.
后与汽车相遇………………………………1分.
在△MON中,MO=500,ON=100t,MN=vt.……………………2分
设∠MON=α,
由题意,知sinα= ,则cosα=
,则cosα= .……………………4分
.……………………4分
由余弦定理,知MN2=OM2+ON2-2OM·ONcosα,
即v2t2=5002+1002t2-2×500×100t× .
.
整理,得v2=(500× -80)2+3 600.……………………7分
-80)2+3 600.……………………7分
当 =
= ,即t=
,即t= 时,vmin2="3" 600.
时,vmin2="3" 600.
∴vmin=60,…………………………………………9
即快艇至少须以60千米/时的速度行驶,此时MN=60× =15×25,MQ=300.
=15×25,MQ=300.
 设∠MNO=β,则sinβ=
设∠MNO=β,则sinβ= =
= .
.
∴cosα=sinβ.
∴α+β=90°,即MN与OM垂直.………………………………12 分
分
t小时
 后与汽车相遇………………………………1分.
后与汽车相遇………………………………1分.在△MON中,MO=500,ON=100t,MN=vt.……………………2分
设∠MON=α,
由题意,知sinα=
 ,则cosα=
,则cosα= .……………………4分
.……………………4分由余弦定理,知MN2=OM2+ON2-2OM·ONcosα,
即v2t2=5002+1002t2-2×500×100t×
 .
.整理,得v2=(500×
 -80)2+3 600.……………………7分
-80)2+3 600.……………………7分当
 =
= ,即t=
,即t= 时,vmin2="3" 600.
时,vmin2="3" 600.∴vmin=60,…………………………………………9
即快艇至少须以60千米/时的速度行驶,此时MN=60×
 =15×25,MQ=300.
=15×25,MQ=300. 设∠MNO=β,则sinβ=
设∠MNO=β,则sinβ= =
= .
.∴cosα=sinβ.
∴α+β=90°,即MN与OM垂直.………………………………12
 分
分略

练习册系列答案
相关题目
 bc.
bc. 的值
的值 站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出.
站C,并在车站C也停留10分钟.已知早上8点时甲车从车站A、乙车从车站B同时开出. ,
, ,
, ,
, )
)
 ,求
,求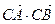 的最大值
的最大值 中,D是BC边上任意一点(D与B,C不重合),且
中,D是BC边上任意一点(D与B,C不重合),且 ,则
,则 ,
, =
= 


 中,
中, ,则
,则 的取值范围是
的取值范围是  中,
中, ,
, ,
, ,则
,则