题目内容
(本题满分12分)在△ABC中,a、b、c分别是角A、B、C所对的边,
且acosB十bcosA="1"
(1)求c
(2)若tan(A+B)= ,求
,求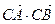 的最大值
的最大值
且acosB十bcosA="1"
(1)求c
(2)若tan(A+B)=
 ,求
,求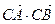 的最大值
的最大值解: (1) 由acosB十bcosA=1及正弦定理,得
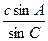 ·cosB+
·cosB+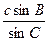 ·cosA=
·cosA= 1,
1,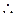 csin(A+B)=sinC,
csin(A+B)=sinC,
又sin(A+B)=" sin" (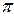 -C)="sinC"
-C)="sinC"  0,
0, 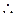 c=1. ……6分
c=1. ……6分
(2)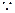 tan(A+B)=
tan(A+B)=  , 0<A+B<
, 0<A+B<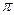 ,
, 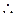 A+B=
A+B=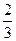
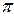
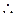 C=
C=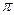 -( A+B)=
-( A+B)= 
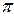
由余弦定理得,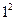 =a
=a +b
+b -2abcosC=a
-2abcosC=a +b
+b -ab
-ab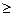 2ab-ab= ab=2
2ab-ab= ab=2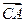 ·
·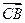
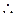
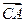 ·
·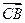
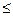
 ,当且仅当a=b=1时取“=”号,
,当且仅当a=b=1时取“=”号,
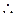
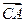 ·
·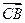 的最大值是
的最大值是 . ……12分
. ……12分
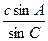 ·cosB+
·cosB+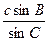 ·cosA=
·cosA= 1,
1,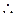 csin(A+B)=sinC,
csin(A+B)=sinC,又sin(A+B)=" sin" (
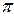 -C)="sinC"
-C)="sinC"  0,
0, 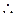 c=1. ……6分
c=1. ……6分(2)
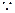 tan(A+B)=
tan(A+B)=  , 0<A+B<
, 0<A+B<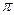 ,
, 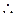 A+B=
A+B=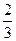
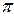
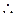 C=
C=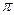 -( A+B)=
-( A+B)= 
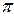
由余弦定理得,
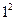 =a
=a +b
+b -2abcosC=a
-2abcosC=a +b
+b -ab
-ab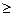 2ab-ab= ab=2
2ab-ab= ab=2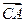 ·
·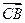
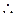
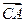 ·
·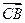
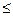
 ,当且仅当a=b=1时取“=”号,
,当且仅当a=b=1时取“=”号,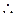
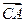 ·
·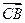 的最大值是
的最大值是 . ……12分
. ……12分略

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 中,若
中,若
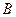 的大小
的大小 ,
, ,求
,求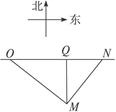
 ,
, ,则A=( )
,则A=( )



 中,侧面
中,侧面 与侧面
与侧面 均是边长为
均是边长为 的正
的正 ,
, 是
是 的中点,
的中点, 平面
平面 ;
; 的余弦值
的余弦值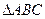 中,
中,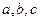 分别为
分别为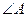 .
.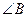 .
.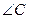 的对边,已知
的对边,已知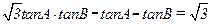 ,
,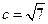 ,
,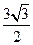 .
.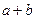 的值.
的值. 中,角
中,角 的对边分别是
的对边分别是 ,已知
,已知 ,则
,则 边,向量m=(
边,向量m=( ),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____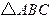 中,
中,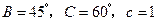 ,则最短边的边长等于
,则最短边的边长等于