题目内容
由不等式组
围成的三角形区域内有一个内切圆,向该三角形区域内随机投一个点,该点落在圆内的概率是关于t的函数P(t),则( )
|
分析:根据题意,分析t的取值范围,再设区域边界的三条直线的交点分别为ABC,结合图形易得△ABC是等腰直角三角形,且AB=7-t,即可得其面积,又由直角三角形的性质,可得其内切圆的半径,进而可得其面积,由几何概型可得点落在圆内的概率,可得求得P(t),由导数的计算可得p′(t),即可得答案.
解答: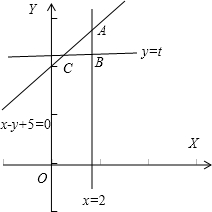 解:根据题意,设直线x-y+5=0与x=2交于点A,易得A(2,7),
解:根据题意,设直线x-y+5=0与x=2交于点A,易得A(2,7),
若不等式组
能围成的三角形区域,易得5<t<7,
则其边界直线为y=t,x-y+5=0,x=2,设x-y+5=0与y=t交于点C,x=2与y=t交于点B,则B(2,t)
分析可得△ABC是等腰直角三角形,且AB=7-t,
则其面积为S=
(7-t)2,
易得内接圆半径r=
,
其面积为S1=
π(2-
)2(7-t)2,
p(t)=
=
,该值与t无关,
所以P′(t)=0.
故选C.
 解:根据题意,设直线x-y+5=0与x=2交于点A,易得A(2,7),
解:根据题意,设直线x-y+5=0与x=2交于点A,易得A(2,7),若不等式组
|
则其边界直线为y=t,x-y+5=0,x=2,设x-y+5=0与y=t交于点C,x=2与y=t交于点B,则B(2,t)
分析可得△ABC是等腰直角三角形,且AB=7-t,
则其面积为S=
| 1 |
| 2 |
易得内接圆半径r=
(2-
| ||
| 2 |
其面积为S1=
| 1 |
| 4 |
| 2 |
p(t)=
| S1 |
| S |
6-4
| ||
| 4 |
所以P′(t)=0.
故选C.
点评:本题考查几何概型的计算,关键在于发现三角形ABC为直角等腰三角形,进而可以求出其面积与内接圆的面积.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
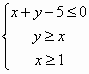 确定,若M(x,y)为区域D上的动点,点A的坐标为(2,3),则z=
确定,若M(x,y)为区域D上的动点,点A的坐标为(2,3),则z=