题目内容
已知函数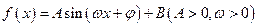 的一系列对应值如下表:
的一系列对应值如下表:
(1)根据表格提供的数据求函数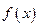 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数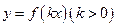 周期为
周期为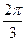 ,当
,当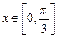 时,方程
时,方程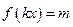 恰有两个不同的解,求实数
恰有两个不同的解,求实数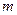 的取值范围;
的取值范围;
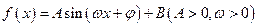 的一系列对应值如下表:
的一系列对应值如下表: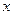 | 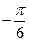 | 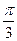 | 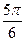 | 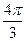 | 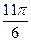 | 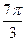 | 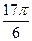 |
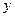 | 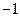 | 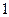 | 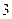 | 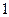 | 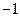 | 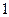 | 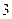 |
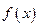 的一个解析式;
的一个解析式;(2)根据(1)的结果,若函数
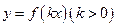 周期为
周期为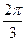 ,当
,当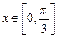 时,方程
时,方程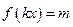 恰有两个不同的解,求实数
恰有两个不同的解,求实数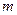 的取值范围;
的取值范围;⑴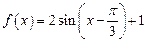 ⑵实数的取值范围是
⑵实数的取值范围是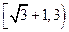
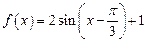 ⑵实数的取值范围是
⑵实数的取值范围是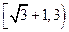
分析图表发现周期性、最值、对称点坐标确定参数.借助数形结合讨论方程的解.
(1)设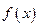 的最小正周期为
的最小正周期为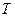 ,得
,得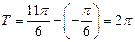 …………………….. 2分
…………………….. 2分
由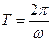 得
得
又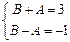 ,解得
,解得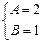 …………………….. 3分
…………………….. 3分
令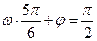 ,即
,即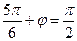 ,解得
,解得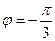
∴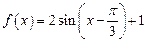 …………………….. 5分
…………………….. 5分
(2)∵函数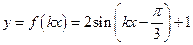 的周期为
的周期为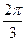
又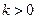 ∴
∴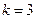 …………………….. 6分
…………………….. 6分
令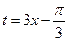 ,∵
,∵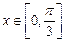 ∴
∴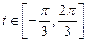 …………………….. 8分
…………………….. 8分
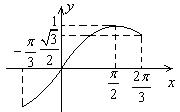
如图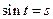 在
在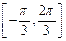 上有两个不同的解的充要条件是
上有两个不同的解的充要条件是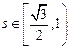
∴方程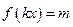 在
在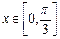 时恰好有两个不同的解的充要条件是
时恰好有两个不同的解的充要条件是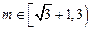 ,
,
即实数的取值范围是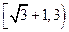 …………………….. 12分
…………………….. 12分
高考中三角函数的大题往往在知识的交汇处入手.
(1)设
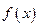 的最小正周期为
的最小正周期为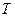 ,得
,得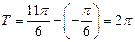 …………………….. 2分
…………………….. 2分
由
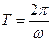 得
得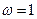
又
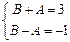 ,解得
,解得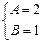 …………………….. 3分
…………………….. 3分令
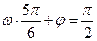 ,即
,即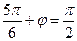 ,解得
,解得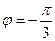
∴
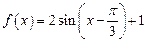 …………………….. 5分
…………………….. 5分(2)∵函数
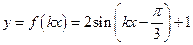 的周期为
的周期为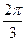
又
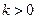 ∴
∴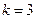 …………………….. 6分
…………………….. 6分令
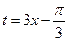 ,∵
,∵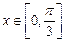 ∴
∴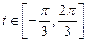 …………………….. 8分
…………………….. 8分如图
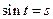 在
在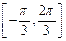 上有两个不同的解的充要条件是
上有两个不同的解的充要条件是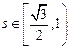
∴方程
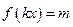 在
在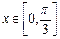 时恰好有两个不同的解的充要条件是
时恰好有两个不同的解的充要条件是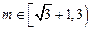 ,
,即实数的取值范围是
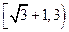 …………………….. 12分
…………………….. 12分高考中三角函数的大题往往在知识的交汇处入手.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
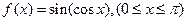 ,求
,求 的最大值与最小值。
的最大值与最小值。 ,f(x)=cosB(
,f(x)=cosB(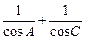 ).
).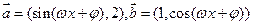 (
(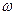 >0,0<
>0,0<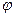 <
<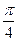 ),函数
),函数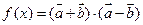 ,
,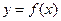 的图象的相邻两对称轴之间的距离为2,且过点
的图象的相邻两对称轴之间的距离为2,且过点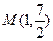 。(1)求
。(1)求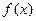 的表达式;(2)求
的表达式;(2)求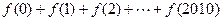 的值。
的值。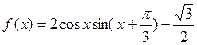 .
.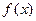 的最小正周期;
的最小正周期;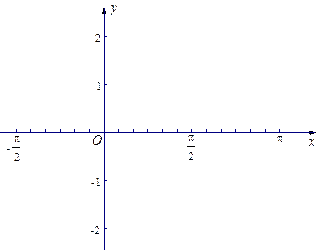
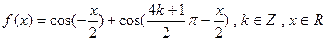 。
。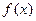 的周期;(2)解析式及
的周期;(2)解析式及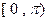 上的减区间;
上的减区间;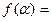
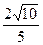 ,
,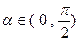 ,求
,求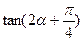 的值。
的值。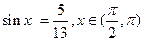 ,求cos2x和
,求cos2x和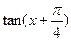 值.
值.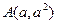 ,
,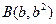
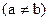 的坐标满足
的坐标满足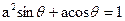 ,
,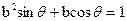 ,则原点到直线AB的距离是___________。
,则原点到直线AB的距离是___________。