题目内容
12.解答题:己知f(x)=1+1ogx3,g(x)=21ogx2,试比较f(x)与g(x)的大小.分析 利用作差法去判断两个函数的大小,通过作出将f(x)-g(x)转化为关于logx3为变量的函数,然后结合函数的性质去判断大小.
解答 解:∵f(x)=1+logx3,g(x)=2logx2,
∴f(x)-g(x)=1+logx3-2logx2=1+logx3-logx4=1+logx$\frac{3}{4}$.
分类讨论:①若1+logx$\frac{3}{4}$=0,即x=$\frac{4}{3}$时,此时f(x)=g(x).
②若1+logx$\frac{3}{4}$<0,即logx$\frac{3}{4}$<-1,解得1<x<$\frac{4}{3}$,此时f(x)<g(x).
③若1+logx$\frac{3}{4}$>0,即logx$\frac{3}{4}$>-1,解得x>$\frac{4}{3}$或0<x<1,此时f(x)>g(x).
综上:①当x=$\frac{4}{3}$时,f(x)=g(x).
②当1<x<$\frac{4}{3}$,时,f(x)<g(x).
③当x>$\frac{4}{3}$或0<x<1,时,f(x)>g(x).
点评 本题考查了利用作差法去判断两个数大小的方法.作差之后如何判断式子的符号,是这类问题的难点.

练习册系列答案
相关题目
20.log483+4log482等于( )
| A. | 1 | B. | 2 | C. | 6 | D. | 48 |
1.设M=${∫}_{1}^{2}$log${\;}_{\frac{1}{2}}$xdx,N=${∫}_{1}^{2}$log${\;}_{\frac{1}{3}}$xdx,则( )
| A. | M>N | B. | M<N | C. | |M|<|N| | D. | |M|=|N| |
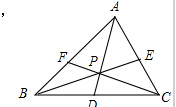 P为△ABC内一点,AP,BP,CP分别交对边于D,E,F.已知AP=BP=CP=6,设PD=x,PE=y,PF=z,xy+yz+zx=28,则xyz=24.
P为△ABC内一点,AP,BP,CP分别交对边于D,E,F.已知AP=BP=CP=6,设PD=x,PE=y,PF=z,xy+yz+zx=28,则xyz=24.