题目内容
已知把向量
﹦(1,1)向右平移两个单位,再向下平移一个单位得到向量
,则
的坐标为
| a |
| b |
| b |
(1,1)
(1,1)
.分析:题目给出了一个平面向量
=(1,1),向量的坐标,指的是以原点为起点的向量终点的坐标,把向量平移后,其起点和终点都随着进行了移动,平移后向量的坐标仍然等于平移后终点的坐标减去起点的坐标.
也可直接根据向量相等的概念,向量平移后其长度和方向均未改变,平移后的向量和原向量是相等的向量,坐标不变.
| a |
也可直接根据向量相等的概念,向量平移后其长度和方向均未改变,平移后的向量和原向量是相等的向量,坐标不变.
解答:解:法一、
如图,
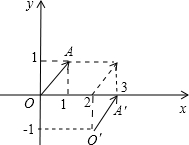
设
=
,因为
=(1,1),所以O(0,0),A(1,1),
向量
向右平移两个单位,再向下平移一个单位后,得到起点O′(2,-1),终点A′(3,0),
即
=
=(3,0)-(2,-1)=(1,1).
故答案为(1,1).
法二、
根据向量相等的概念,向量
=(1,1)在平面内无论如何平移,只要平移过程中模不变,且方向不发生变化,得到的向量与原向量都是相等的向量,相等的向量坐标相等,所以,向量
向右平移两个单位,再向下平移一个单位后,
得到的向量
=(1,1).
故答案为(1,1).
如图,

设
| OA |
| a |
| a |
向量
| a |
即
| b |
| O′A′ |
故答案为(1,1).
法二、
根据向量相等的概念,向量
| a |
| a |
得到的向量
| b |
故答案为(1,1).
点评:本题考查了平面向量的坐标运算,考查了向量相等的概念,向量的坐标,指的是以原点为起点的向量的终点坐标,此题是基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
已知
=(0,1)、
=(0,3),把向量
绕点A逆时针旋转90°得到向量
,则向量
等于( )
| OA |
| OB |
| AB |
| AC |
| OC |
| A、(-2,1) |
| B、(-2,0) |
| C、(3,4) |
| D、(3,1) |