题目内容
已知函数
(Ⅰ)若对任意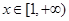 ,使得
,使得 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)证明:对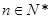 ,不等式
,不等式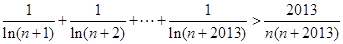 成立.
成立.
(Ⅰ)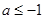 (Ⅱ)详见解析.
(Ⅱ)详见解析.
解析试题分析:(Ⅰ) 利用导数分析单调性,进而求最值;(Ⅱ)利用不等式的放缩和数列的裂项求和
试题解析:(I) 化为
化为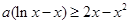
易知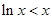 ,
,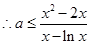 ,设
,设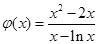
 ,设
,设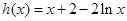 ,
,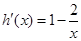
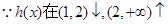 ,
,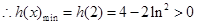
 ,
, 上是增函数,
上是增函数,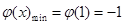
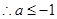
(Ⅱ)由(I)知: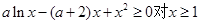 恒成立,
恒成立,
令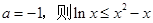 ,
,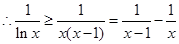
取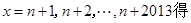
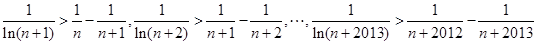
相加得: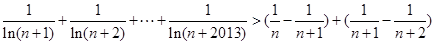
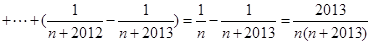
即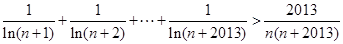
证明完毕
考点:查导数,函数的单调性,数列求和,不等式证明

练习册系列答案
相关题目
题目内容
已知函数
(Ⅰ)若对任意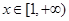 ,使得
,使得 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)证明:对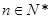 ,不等式
,不等式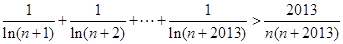 成立.
成立.
(Ⅰ)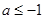 (Ⅱ)详见解析.
(Ⅱ)详见解析.
解析试题分析:(Ⅰ) 利用导数分析单调性,进而求最值;(Ⅱ)利用不等式的放缩和数列的裂项求和
试题解析:(I) 化为
化为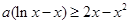
易知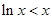 ,
,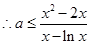 ,设
,设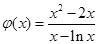
 ,设
,设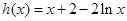 ,
,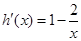
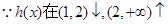 ,
,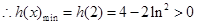
 ,
, 上是增函数,
上是增函数,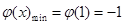
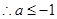
(Ⅱ)由(I)知: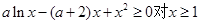 恒成立,
恒成立,
令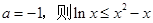 ,
,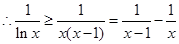
取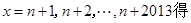
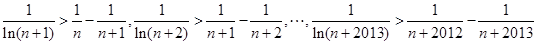
相加得: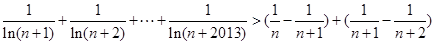
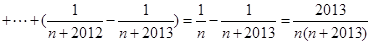
即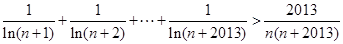
证明完毕
考点:查导数,函数的单调性,数列求和,不等式证明
