题目内容
2.已知椭圆$C:\frac{x^2}{49}+\frac{y^2}{24}=1$的左右焦点分别为F1,F2,C上一点P满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0$,则△PF1F2的内切圆面积为4π.分析 根据椭圆的方程,算出a=5且焦距|F1F2|=2c=10.设|PF1|=m,|PF2|=n,根据椭圆的定义和勾股定理建立关于m、n的方程组,平方相减即可求出|PF1|•|PF2|=48,结合直角三角形的面积公式,可得△PF1F2的面积S=$\frac{1}{2}$|PF1|•|PF2|=24,再由S=$\frac{1}{2}$r(|PF1|+|PF2|+|F1F2|),求得r,即可得到所求内切圆的面积.
解答 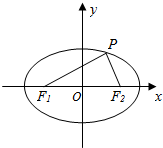 解:∵椭圆$C:\frac{x^2}{49}+\frac{y^2}{24}=1$,
解:∵椭圆$C:\frac{x^2}{49}+\frac{y^2}{24}=1$,
∴a2=49,b2=24,可得c2=a2-b2=25,即a=7,c=5,
设|PF1|=m,|PF2|=n,则有m+n=2a=14,m2+n2=(2c)2=100,
可得2mn=96,即mn=48,
∴|PF1|•|PF2|=48,
∵PF1⊥PF2,得∠F1PF2=90°,
∴△PF1F2的面积S=$\frac{1}{2}$|PF1|•|PF2|=$\frac{1}{2}$×48=24,
由S=$\frac{1}{2}$r(|PF1|+|PF2|+|F1F2|)=$\frac{1}{2}$r•(2a+2c)=12r(r为内切圆的半径),
由12r=24,解得r=2,则所求内切圆的面积为4π.
故答案为:4π.
点评 本题给出椭圆的焦点三角形为直角三角形,求它的面积,着重考查了勾股定理、椭圆的定义和简单几何性质等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的函数是( )
| A. | y=x3 | B. | $y=|{log_2^{\;}x}|$ | C. | y=2|x| | D. | y=-x2+1 |
11.已知数列{an}满足${a_1}+{a_2}+…+{a_n}={n^3}$,则a6+a7+a8+a9=( )
| A. | 729 | B. | 367 | C. | 604 | D. | 854 |
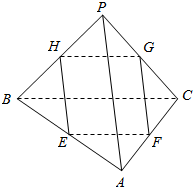 如图所示,在三棱锥P-ABC中,PA=4,BC=6,与PA、BC都平行的截面四边形EFGH的周长为l,试确定l的取值范围.
如图所示,在三棱锥P-ABC中,PA=4,BC=6,与PA、BC都平行的截面四边形EFGH的周长为l,试确定l的取值范围.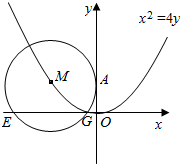 设圆M过点A(0,2),且圆心M在曲线C:x2=4y上,EG是圆M在x轴上截得的弦,试探究当M运动时.弦长|EG|是否为定值?为什么?
设圆M过点A(0,2),且圆心M在曲线C:x2=4y上,EG是圆M在x轴上截得的弦,试探究当M运动时.弦长|EG|是否为定值?为什么?