题目内容
(本小题满分12分)已知y= 是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
(1)求 的解析式;
的解析式;
(2)求函数 的单调递减区间及值域..
的单调递减区间及值域..
 是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1(1)求
 的解析式;
的解析式;(2)求函数
 的单调递减区间及值域..
的单调递减区间及值域.. (1) ;(2)单调递减区间为(1 ,4) .值域
;(2)单调递减区间为(1 ,4) .值域
 ;(2)单调递减区间为(1 ,4) .值域
;(2)单调递减区间为(1 ,4) .值域
本题主要考查用待定系数法求函数解析式,这类题目,一般是在定型之后,通常采用的方法.
(1)先由二次函数,设出其解析式,再利用f(0)=8,求得c,再利用待定系数法应用f(x+1)-f(x)=-2x+1求解.
(2)由(1)写出函数f(x)的表达式,结合对数函数的性质得出其单调递减区间及值域即可.
解:(1)设 f(0)=8得c=8
f(0)=8得c=8
f(x+1)-f(x)=-2x+1得 a=-1,b=2

(2) =
=
当 时,
时,
单调递减区间为(1 ,4) .值域
(1)先由二次函数,设出其解析式,再利用f(0)=8,求得c,再利用待定系数法应用f(x+1)-f(x)=-2x+1求解.
(2)由(1)写出函数f(x)的表达式,结合对数函数的性质得出其单调递减区间及值域即可.
解:(1)设
 f(0)=8得c=8
f(0)=8得c=8 f(x+1)-f(x)=-2x+1得 a=-1,b=2

(2)
 =
=
当
 时,
时,
单调递减区间为(1 ,4) .值域


练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 的顶点坐标为
的顶点坐标为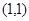 ,且
,且 ,
, ∈
∈ ,
, 的图象恒在
的图象恒在 的图象上方,
的图象上方, 的取值范围,
的取值范围, 上单调,求实数
上单调,求实数 的取值范围.
的取值范围. 满足条件
满足条件 ,及
,及 .
. 上的最大和最小值.
上的最大和最小值. ,设函数
,设函数 ,
, ,且函数
,且函数 的值域为
的值域为 ,求
,求 在
在 上是单调函数,求实数
上是单调函数,求实数 的取值范围.
的取值范围. ax2+3x+5(a>0).
ax2+3x+5(a>0). 的单调增区间为 ;
的单调增区间为 ;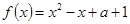
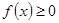 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。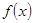 在区间
在区间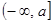 上的最小值
上的最小值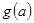 的表达式。
的表达式。
 时,求函数的最大值和最小值;
时,求函数的最大值和最小值;  的取值范围,使
的取值范围,使 在区间
在区间 上是单调函数。
上是单调函数。
 , 若
, 若 在区间
在区间 上的最大值为
上的最大值为 , 最小值为
, 最小值为 , 令
, 令 .
.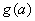 的函数表达式;
的函数表达式;