题目内容
15.已知函数f(x)=$\frac{t+sinx}{t+cosx}({|t|>1})$的最大值和最小值分别是M,m,则M•m为1.分析 首先,根据所给函数结构形式,得到动点A(cosθ,sinθ)与点B(-t,-t)的连线的斜率k,然后,借助于直线与圆的位置关系,确定M和m的值即可.
解答 解:由函数f(x)=$\frac{t+sinx}{t+cosx}({|t|>1})$,
得:动点A(cosθ,sinθ)与点B(-t,-t)的连线的斜率k,
点A在单位圆上运动,点B则在直线y=x上,|x|>1,且在单位圆外,
当直线AB与单位圆相切时,此时k取得最大值和最小值,
设AB:y+t=k(x+t),
即kx-y+(k-1)t=0,
它到原点的距离为1,
∴$\frac{|k-1||t|}{\sqrt{1+{k}^{2}}}=1$,
∴[(k-1)t]2=1+k2,
∴(t2-1)k2-2t2k+t2-1=0,
∴k=$\frac{{t}^{2}±\sqrt{2{t}^{2}-1}}{{t}^{2}-1}$,
∴M=$\frac{{t}^{2}+\sqrt{2{t}^{2}-1}}{{t}^{2}-1}$,
m=$\frac{{t}^{2}-\sqrt{2{t}^{2}-1}}{{t}^{2}-1}$,
∴M•m=1.
故答案为:1.
点评 本题重点考查了等价转化思想、斜率公式及其运用、直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
6.函数f($\frac{1}{x}$)=$\frac{1}{1+x}$,则函数f(x)的解析式是 ( )
| A. | $\frac{x}{x+1}$ (x≠0) | B. | 1+x | C. | $\frac{1+x}{x}$ | D. | $\frac{1}{x+1}$(x≠0) |
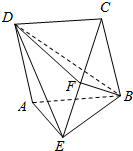 如图,已知矩形ABCD,BC⊥平面ABE,F为CE的中点.
如图,已知矩形ABCD,BC⊥平面ABE,F为CE的中点.