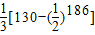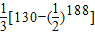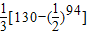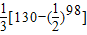题目内容
把公差d=2的等差数列{an}的各项依次插入等比数列{bn}中,将{bn}按原顺序分成1项,2项,4项,…,2n-1项的各组,得到数列{cn}:b1,a1,b2,b3,a2,b4,b5,b6,b7,a3,…,若{cn}的前n项的和为Sn,且c1=1,c2=2,S3=
,则S100等于( )
| 13 |
| 4 |
分析:由已知我们可分析出{cn}的前100项中,含等差数列{an}的前6项,等比数列{bn}的前94项,分别利用等差、等比数列的前n和公式可得答案.
解答:解:由题意得{cn}是an前(包括an)共有(1+1)+(2+1)+(4+1)+…+(2n-1+1)=2n+n-1项
∵n=6时,2n+n-1=69<100,n=7时,2n+n-1=134>100,
故{cn}的前100项中,含等差数列{an}的前6项,等比数列{bn}的前94项,
由已知中c1=1,c2=2,S3=
,可得
等差数列{an}的公差d=2,首项a1=c2=2,
等比数列{bn}的首项b1=c1=1,b2=S3-c1-c2=
,即公比q=
,
∴S100=(2+4+…+12)+(1+
+…+
)=
[130-(
)186]
故选A
∵n=6时,2n+n-1=69<100,n=7时,2n+n-1=134>100,
故{cn}的前100项中,含等差数列{an}的前6项,等比数列{bn}的前94项,
由已知中c1=1,c2=2,S3=
| 13 |
| 4 |
等差数列{an}的公差d=2,首项a1=c2=2,
等比数列{bn}的首项b1=c1=1,b2=S3-c1-c2=
| 1 |
| 4 |
| 1 |
| 4 |
∴S100=(2+4+…+12)+(1+
| 1 |
| 4 |
| 1 |
| 493 |
| 1 |
| 3 |
| 1 |
| 2 |
故选A
点评:本题考查的知识点是等差数列和等比数列的前n项和公式,其中第一步分析{cn}的前100项中,含等差数列{an}的前6项,等比数列{bn}的前94项,难度较大.

练习册系列答案
相关题目
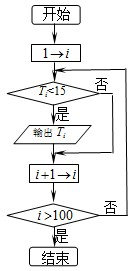 把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=2,S3=
把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=2,S3= 是首项为19,公差d=-2的等差数列,
是首项为19,公差d=-2的等差数列, 为
为 及
及 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列 的通项公式及其前n项和
的通项公式及其前n项和
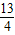 ,则S100等于( )
,则S100等于( )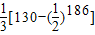
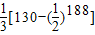


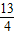 ,则S100等于( )
,则S100等于( )