题目内容
 把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=2,S3=
把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=2,S3=| 13 | 4 |
(1)求数列{an}、{bn}的通项公式;
(2)求数列{cn}的第2010项c2010;
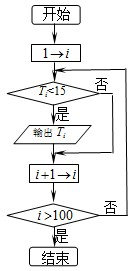
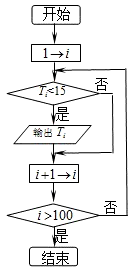
(3)设Tn=2010•bn+an,阅读框图写出输出项,并说明理由.
分析:(1)根据题意,c1=b1=1,c2=a1=2,再根据S3可以计算出b2=
,从而得出等比数列{bn}的公比,最后根据等差数列和等比数列的通项公式,求出数列{an}、{bn}的通项公式;
(2)数列{cn}中各项的特征:{cn}中的第2k(k为正整数)项即数列{an}中的第k项,从而得出c2010=a1005=2010;
(3)由(1)中{an}、{bn}的通项公式,得出Tn=2010•(
)n-1+2n,得出Tn+1的表达式,通过计算Tn+1与Tn+的差,
发现当n>5时Tn+1-Tn>0,{Sn}递增,当n≤5时Tn+1-Tn<0,{Sn}递减满.由以上分析可得:满足条件Tn<15的项只有两项:T6,T7.
| 1 |
| 4 |
(2)数列{cn}中各项的特征:{cn}中的第2k(k为正整数)项即数列{an}中的第k项,从而得出c2010=a1005=2010;
(3)由(1)中{an}、{bn}的通项公式,得出Tn=2010•(
| 1 |
| 4 |
发现当n>5时Tn+1-Tn>0,{Sn}递增,当n≤5时Tn+1-Tn<0,{Sn}递减满.由以上分析可得:满足条件Tn<15的项只有两项:T6,T7.
解答:解:(1)由题意,b1=1,a1=2,
S3=b1+a1+b2=
,故b2=
…(1分)
所以an=2n,bn=(
)n-1…(2分),总计(3分)
(2)数列{cn}中的第2010项即数列{an}中的第1005项,
于是c2010=a1005=2010;…(3分)
(3)由于Tn=2010•(
)n-1+2n
所以Tn+1=2010•(
)n+2n+2
∴Tn+1-Tn=-2010•(
)n-1•
+2=2-6030•(
)n
当n>5时Tn+1-Tn>0{Sn}递增
当n≤5时Tn+1-Tn<0{Sn}递减
通过计算T4=39.41,T5=17.85,T6=13.96,T7=14.49,T8=16.12
所以满足条件Tn<15的项只有两项:T6,T7…(4分)
S3=b1+a1+b2=
| 13 |
| 4 |
| 1 |
| 4 |
所以an=2n,bn=(
| 1 |
| 4 |
(2)数列{cn}中的第2010项即数列{an}中的第1005项,
于是c2010=a1005=2010;…(3分)
(3)由于Tn=2010•(
| 1 |
| 4 |
所以Tn+1=2010•(
| 1 |
| 4 |
∴Tn+1-Tn=-2010•(
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
当n>5时Tn+1-Tn>0{Sn}递增
当n≤5时Tn+1-Tn<0{Sn}递减
通过计算T4=39.41,T5=17.85,T6=13.96,T7=14.49,T8=16.12
所以满足条件Tn<15的项只有两项:T6,T7…(4分)
点评:本题考查了数列与不等式的综合,以及数列的函数特征,属于难题.深刻理解等差数列与等比数列的区别与联系,准确运用通项公式,研究数列的单调性,是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=2,S3=
把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=2,S3= .
.