题目内容
17.①当α∈(0,$\frac{π}{2}$),求证:sinα<α<tanα;①当α∈(0,$\frac{π}{2}$),求证:sinα+cosα>1.
分析 ①由题意作出三角函数线,通过三角形的面积以及扇形面积的大小比较可得.
②作出三角函数线,由三角形两边之和大于第三边可得结论.
解答 解:①在直角坐标系中结合单位圆作出锐角α的正弦线和正切线,
由图可知sinα=MP,α=$\widehat{AP}$,tanα=AT,
∵S△AOP=$\frac{1}{2}$×MP×1=$\frac{1}{2}$sinα,S扇形AOP=$\frac{1}{2}$×$\widehat{AP}$×1=$\frac{1}{2}$α,S△AOT=$\frac{1}{2}$×AT×1=$\frac{1}{2}$tanα,S△AOP<S扇形AOP<S△AOT,
∴MP<$\widehat{AP}$<AT,即sinα<α<tanα,
故答案为:sinα<α<tanα.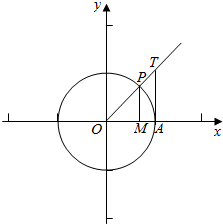
②如图P为α与单位圆交点,
则OP=1,OM、MP分别为α的余弦线,正弦线,
由三角形两边之和大于第三边可得OM+MP>OP,
即sinα+cosα>1.
点评 本题考查三角函数线,考查转化思想以及判断能力,属中档题.

练习册系列答案
相关题目
8.若直线y=kx-1与双曲线x2-y2=1的左支有两个公共点,则k的取值范围是( )
| A. | (-$\sqrt{2}$,0) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-$\sqrt{2}$,-1) | D. | (-$\sqrt{2}$,-1] |
12.设函数f(x)=x3(x∈R),当0≤θ≤$\frac{π}{2}$时,f(cos2θ+2msinθ)+f(-2m-2)<0恒成立,则实数m的取值范围是( )
| A. | (0,1) | B. | (-$\frac{1}{2}$,1) | C. | (-∞,1) | D. | (-$\frac{1}{2}$,+∞) |
2.如果棱长为2$\sqrt{2}$的正四面体的顶点都在一个球面上,那么这个球的表面积是( )
| A. | 8π | B. | 12π | C. | 16π | D. | 20π |
6.函数f(x)=$\sqrt{x+1}$+ln(4-x)的定义域为( )
| A. | [-1,4) | B. | (-1,+∞) | C. | (-1,4) | D. | (4,+∞) |
 如图,函数f(x)的图象为折线 AC B,则不等式f(x)≥log2(x+1)的解集是(-1,1].
如图,函数f(x)的图象为折线 AC B,则不等式f(x)≥log2(x+1)的解集是(-1,1].