题目内容
(2012•漳州模拟)3月是植树造林的最佳时节,公园打算在3.12植树节前后引种一批名优树种.现有甲、乙两家苗木场各送来一批同种树苗.公园园林部分别各抽取100棵测量其高度,得到如下的频率分布表:
(Ⅰ)分别算出甲、乙两家苗木场树苗样本高度的平均值
甲,
乙;
(样本数据第i组的频率为pi,中间值为xi(i=1,2,…,n),则平均值为
=x1p1+x2p2+…+xnpn.)
(Ⅱ)根据样本数据可算得两个方差:
=120.16,
=105.0,结合(Ⅰ)中算出的数据,如果你是公园园林部主管,你将选择哪家苗木场的树苗?说明你的观点;
(Ⅲ)用分层抽样方法从乙苗木场的样本中抽取10棵,小林同学从这10棵中挑选2棵试种,其中高度在[90,100]范围的有X棵,求X的分布列和数学期望.
| 高度(cm) | [60,70) | [70,80) | [80,90) | [90,100] | |
| 频 率 |
甲苗木场 | 0.18 | 0.24 | 0.26 | 0.32 |
| 乙苗木场 | 0.20 | 0.30 | 0.30 | 0.20 | |
. |
| X |
. |
| X |
(样本数据第i组的频率为pi,中间值为xi(i=1,2,…,n),则平均值为
. |
| X |
(Ⅱ)根据样本数据可算得两个方差:
| S | 2 甲 |
| S | 2 乙 |
(Ⅲ)用分层抽样方法从乙苗木场的样本中抽取10棵,小林同学从这10棵中挑选2棵试种,其中高度在[90,100]范围的有X棵,求X的分布列和数学期望.
分析:(Ⅰ)根据平均值为
=x1p1+x2p2+…+xnpn,即可算出甲、乙两家苗木场树苗样本高度的平均值
甲,
乙;
(Ⅱ)观点一:选择乙场的树苗,因为其提供的树苗高度方差较小,成长较整齐,种在公园里比较好看.
观点二:选择甲场的树苗,因为其提供的树苗平均高度较大,说明长势较好,且方差较大,种在公园里显得高矮错落有致,更能体现空间美感.
(Ⅲ)10棵中高度在[90,100]的有2棵,X可取值为0,1,2,X服从超几何分布,,计算其概率,可得X的分布列和数学期望.
. |
| X |
. |
| X |
. |
| X |
(Ⅱ)观点一:选择乙场的树苗,因为其提供的树苗高度方差较小,成长较整齐,种在公园里比较好看.
观点二:选择甲场的树苗,因为其提供的树苗平均高度较大,说明长势较好,且方差较大,种在公园里显得高矮错落有致,更能体现空间美感.
(Ⅲ)10棵中高度在[90,100]的有2棵,X可取值为0,1,2,X服从超几何分布,,计算其概率,可得X的分布列和数学期望.
解答:解:(Ⅰ)
甲=65×0.18+75×0.24+85×0.26+95×0.32=82.2,
乙=65×0.20+75×0.30+85×0.30+95×0.20=80.0,
(Ⅱ)观点一:选择乙场的树苗,因为其提供的树苗高度方差较小,成长较整齐,种在公园里比较好看.
观点二:选择甲场的树苗,因为其提供的树苗平均高度较大,说明长势较好,且方差较大,种在公园里显得高矮错落有致,更能体现空间美感.
(注:两种观点各有其理,只要能依据统计数据说明自己的观点,一样得分.)
(Ⅲ)10棵中高度在[90,100]的有2棵,X可取值为0,1,2,X服从超几何分布,
P(X=0)=
=
,P(X=1)=
=
,P(X=2)=
=
,
故X的分布列为:
E(X)=0×
+1×
+2×
=
.
. |
| X |
. |
| X |
(Ⅱ)观点一:选择乙场的树苗,因为其提供的树苗高度方差较小,成长较整齐,种在公园里比较好看.
观点二:选择甲场的树苗,因为其提供的树苗平均高度较大,说明长势较好,且方差较大,种在公园里显得高矮错落有致,更能体现空间美感.
(注:两种观点各有其理,只要能依据统计数据说明自己的观点,一样得分.)
(Ⅲ)10棵中高度在[90,100]的有2棵,X可取值为0,1,2,X服从超几何分布,
P(X=0)=
| ||||
|
| 28 |
| 45 |
| ||||
|
| 16 |
| 45 |
| ||||
|
| 1 |
| 45 |
故X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 28 |
| 45 |
| 16 |
| 45 |
| 1 |
| 45 |
| 2 |
| 5 |
点评:本题考查统计知识,考查离散型随机变量的分布列与期望,正确运用公式是关键.

练习册系列答案
相关题目
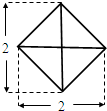 (2012•漳州模拟)一个几何体的正视图、侧视图、俯视图都是如图所示正方形及其对角线,则该几何体的体积等于( )
(2012•漳州模拟)一个几何体的正视图、侧视图、俯视图都是如图所示正方形及其对角线,则该几何体的体积等于( ) (2012•漳州模拟)如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( )
(2012•漳州模拟)如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图,其中第二组月收入在[1.5,2)千元的频数为300,则此次抽样的样本容量为( )